short notes to inform experimental work

Arturo Tozzi  

Former Center for Nonlinear Science, Department of Physics, University of North Texas, Denton, Texas, USA

Former Computationally Intelligent Systems and Signals, University of Manitoba, Winnipeg, Canada

ASL Napoli 1 Centro, Distretto 27, Naples, Italy         

 

Tozziarturo@libero.it

 

 

For years, I have published across diverse academic journals and disciplines, including mathematics, physics, biology, neuroscience, medicine, philosophy, literature.  Now, having no further need to expand my scientific output or advance my academic standing, I have chosen to shift my approach.  Instead of writing full-length articles for peer review, I now focus on recording and sharing original ideas, i.e., conceptual insights and hypotheses that I hope might inspire experimental work by researchers more capable than myself.  I refer to these short pieces as nugae, a Latin word meaning “trifles”, “nuts” or “playful thoughts”.  I invite you to use these ideas as you wish, in any way you find helpful.  I ask only that you kindly cite my writings, which are accompanied by a DOI for proper referencing.   

 

 

 

 

 

 

 

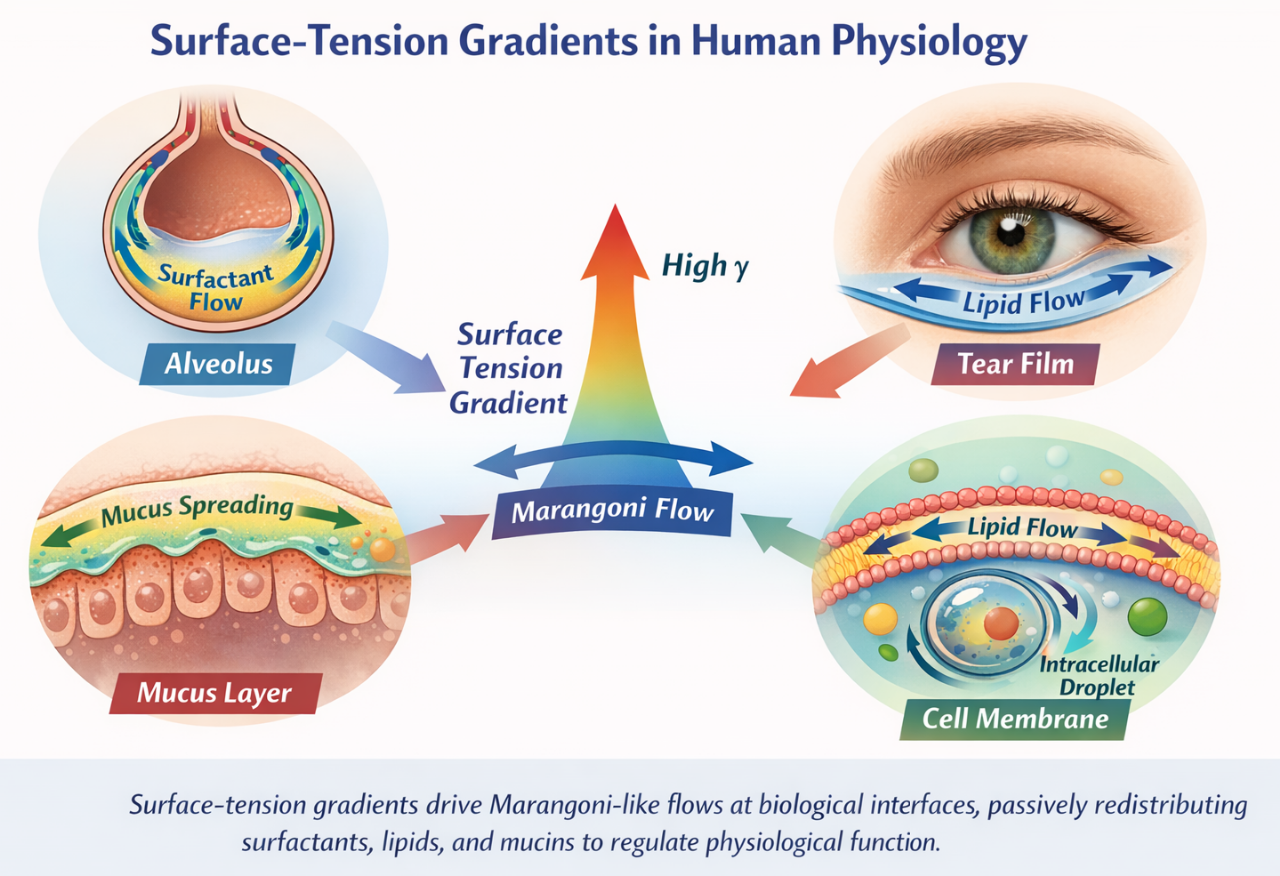
NUGAE - SURFACE-TENSION GRADIENTS AS A PASSIVE REGULATORY LAYER IN HUMAN PHYSIOLOGY

Physiological research has extensively characterized fluid behavior in organs like the lung, eye and gastrointestinal tract, focusing primarily on biochemical composition, elasticity, active transport and molecular regulation, while surface tension is routinely acknowledged as a static parameter or a local constraint. This state of the art lacks a unifying interpretation of how spatial gradients in surface or interfacial tension might act as an active physical driver shaping physiological organization across systems.

 

We suggest to treat surface-tension gradients as a pervasive, passive regulatory mechanism operating at soft biological interfaces. Whenever compositional, thermal or chemical heterogeneities arise along an interface, interfacial stresses necessarily emerge and drive lateral fluid motion, a process known as Marangoni flow, namely the spontaneous movement of fluid along an interface from regions of lower surface tension toward regions of higher surface tension. Our framework emphasizes that these Marangoni-like flows are not marginal physical curiosities but natural consequences of heterogeneous biological interfaces rich in surfactants, lipids, proteins and polymers. In this view, alveolar surfactant redistribution, tear-film spreading after blinking, mucus repair in the gastrointestinal tract and tension equilibration along cellular membranes can all be interpreted as manifestations of the same physical principle. These flows could act to smooth heterogeneities, redistribute material and stabilize function without requiring active energy expenditure or centralized control. Because the driving force is geometric and interfacial rather than biochemical, the same logic could apply across scales, from subcellular droplets to organ-level fluid layers.

 

Our framework could explain robustness and rapid recovery in physiological systems without invoking additional signaling pathways and naturally accounts for scale invariance and energetic efficiency. By focusing on gradients rather than absolute values, our approach also clarifies why small compositional perturbations can trigger large spatial reorganizations.  Our approach is experimentally testable. Surface-tension gradients can be measured or inferred using microtensiometry, tracer particle velocimetry and controlled perturbations of surfactant composition in ex vivo or in vitro models. Testable predictions include the emergence of lateral interfacial flows following localized surfactant depletion, predictable relaxation times that scale with interface size and viscosity and pathological sensitivity when gradient-driven equilibration is impaired.

 

We argue that physiology could include a previously underappreciated layer of passive control that reduces regulatory burden on active systems. This perspective opens avenues for reinterpreting diseases as failures of interfacial equilibration, guiding therapeutic strategies that restore gradients rather than targeting single molecules. For instance, the impairment of Marangoni-like mechanisms could contribute to explain the onset of dry eye disease. Future research can extend this logic to developmental biology, tissue engineering and synthetic biomimetic systems, where designing appropriate interfacial gradients may achieve functional organization with minimal energetic cost.

 

QUOTE AS:  Tozzi A.  2026. Nugae - surface-tension gradients as a passive regulatory layer in human physiology. DOI: 10.13140/RG.2.2.19433.35684

 

 

 

 

 

 

 

 

 

 

 

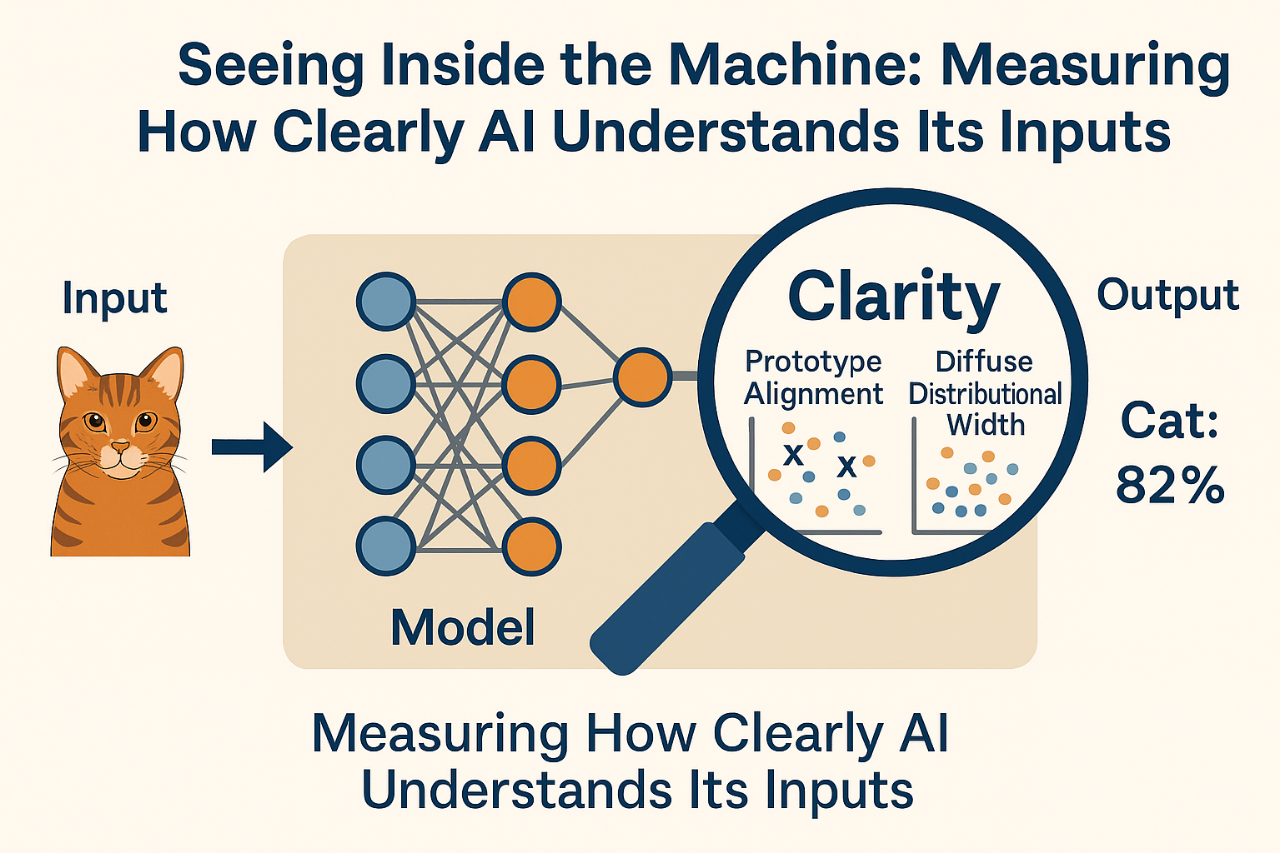
BLURREDNESS AS REPRESENTATIONAL FAILURE: RAMSEY-INSPIRED METRICS FOR INTERNAL CLARITY IN AI JUDGMENT

 

Modern artificial intelligence (AI) systems are increasingly deployed in sensitive domains like healthcare, finance and autonomous technologies, where reliable decision-making is crucial. Today, most approaches to AI reliability focus on how confident the system is in its predictions. Methods such as Bayesian networks, dropout-based approximations and ensemble learning attempt to quantify uncertainty, mainly by analyzing the output probabilities. However, these techniques often overlook a key issue: whether the internal representation of the input itself is meaningful or clear. A model might feel “confident” in its output, while internally holding a confused or distorted view of what it was asked to process.

 

To address this gap, we propose a new approach inspired by the work of philosopher Frank P. Ramsey. In an unpublished manuscript preserved in the Frank P. Ramsey Papers (University of Pittsburgh Archives of Scientific Philosophy, Box 2, Folder 24), he introduced the idea of blurredness. i.e., the notion that a belief may be unclear not because the object is uncertain, but because the representation of that object is internally vague or unfocused. He was among the first to shift attention away from what is known toward how clearly it is represented.  This insight can be translated into the realm of machine learning: even if an AI model is technically confident, it may still be acting on “blurry” internal perceptions.  Building on this idea, a method can be built aiming to quantify representational clarity inside a model, focusing on how input data are structured in the model’s latent (hidden) space.  Two main metrics can be proposed:

 

a) Prototype Alignment – This measures how closely a model’s internal representation of an input matches the central example of its predicted class.

b) Latent Distributional Width – This captures how tightly or loosely clustered similar inputs are, indicating the precision or “blur” of internal categories.

 

Unlike traditional uncertainty methods, this approach works inside the network, offering a diagnostic tool helping identify whether the model’s “understanding” is structurally sound.  This internal perspective has several potential advantages. It may enable earlier detection of model failures, reveal why models perform poorly under certain conditions and guide training toward more robust internal reasoning.  It also opens new experimental directions: for instance, testing whether models with high clarity scores resist adversarial examples better, or whether clarity metrics can predict generalization on unseen data.

 

By incorporating Ramsey’s philosophical insight into AI, we gain a richer understanding of what it means for a machine to know clearly—not just predict correctly.

 

 

 

QUOTE AS:  Tozzi, Arturo. 2025. Blurredness as Representational Failure: Ramsey-Inspired Metrics for Internal Clarity in AI Judgment. July. https://doi.org/10.13140/RG.2.2.28329.51042.

 

 

 

 

 

 

 

 

 

 

 

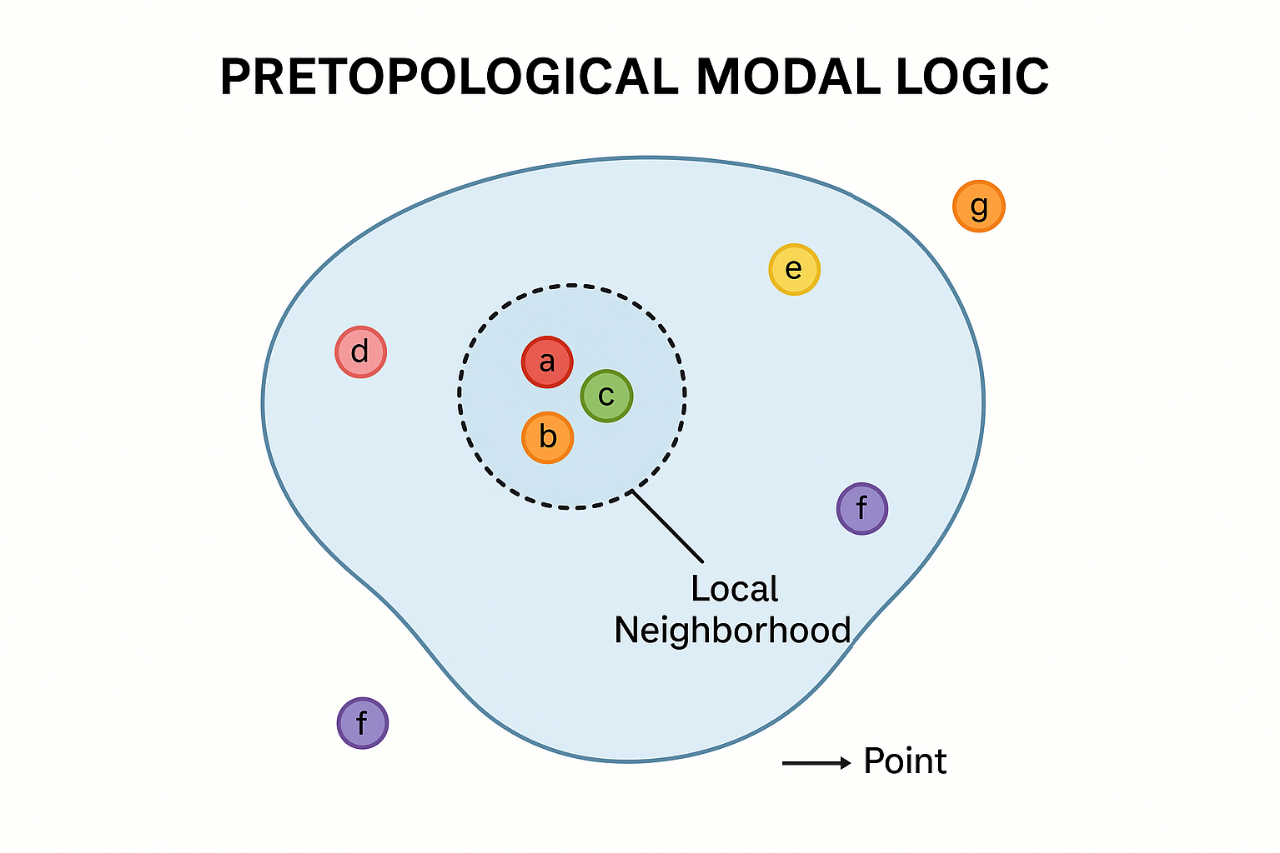
A PRETOPOLOGICAL APPROACH TO MODAL REASONING: A NEW LOGICAL APPROACH IN CONTEXTS WHERE ONLY PARTIAL OR LOCALLY AVAILABLE KNOWLEDGE IS RELEVANT

In many scientific and technological settings—from distributed computing and sensor networks to biological systems and artificial intelligence—agents must make decisions based on partial, local, or uncertain information. Traditional modal logic has long been used to reason about such knowledge and possibility, often relying on structures like Kripke frames or generalized neighborhood models. However, these existing methods either assume too much global structure (as in Kripkean accessibility relations) or allow too much arbitrariness (as in unconstrained neighborhood semantics), which can make them unsuitable for systems grounded in limited, local knowledge.

To bridge this gap, we propose a new method: Pretopologically-Neighborhood Modal Logic (PNML). This approach grounds modal reasoning in pretopological spaces, a mathematical framework that maintains minimal but essential structure. In pretopology, each point (or world) is assigned a set of neighborhoods that satisfy two simple rules: they must include the point itself and be upward closed (i.e., containing larger sets if they contain a smaller one). Unlike traditional topology, this framework does not require closure under intersection—making it flexible enough to model fragmented, disjoint, or observer-relative perspectives.  In PNML, modal statements are interpreted locally: something is “necessarily true” at a point only if it is true across at least one of its valid neighborhoods. This reflects how real agents (such as cells, nodes in a network, or decision-makers) operate with local snapshots of their environments. Unlike many standard modal systems, PNML avoids the rule of necessitation and does not enforce strong global inference rules. This allows it to represent weak, non-normal, and dynamic forms of reasoning under uncertainty.

The novelty of this logic lies in its balance between minimal structure and formal rigor. It offers a logically complete, semantically sound framework that respects informational constraints without sacrificing analytic clarity. Compared to topological logics, it is less rigid; compared to standard neighborhood models, it is more disciplined.  PNML opens new research directions and applications. In biology, it could model how cells make decisions based on local signaling. In computing, it can capture agent-based protocols with restricted information access. Future research might include modal updates over time, multi-agent extensions, and formal proof systems aligned with PNML’s structure. Experiments could compare PNML’s modeling accuracy with classical logic in systems like belief revision or distributed diagnostics, testing its advantage in scenarios of local, partial observability.

In short, PNML offers a fresh way to model reasoning in real-world systems where knowledge is local, partial, and structured—yet never fully global.

QUOTE AS: Tozzi A. 2025. Pretopological Modal Logic for Local Reasoning and Uncertainty. Preprints. https://doi.org/10.20944/preprints202506.1902.v1  

 

 

 

 

 

 

 

BLACK HOLES AS QUANTUM RESERVOIR COMPUTERS: A NEW COMPUTATIONAL PERSPECTIVE ON GRAVITY

We introduce a new approach for understanding spacetime not just as geometry, but as an active substrate for quantum computation and learning.

For years, I have published across a wide range of journals and disciplines, including mathematics, physics, biology, neuroscience, medicine and philosophy. Now, having no further need to expand my scientific output or advance my academic standing, I have chosen to shift my approach.  Instead of writing full-length articles for peer review, I now focus on recording and sharing original ideas, i.e., conceptual insights and hypotheses that I hope might inspire experimental work by researchers more capable than myself.  I refer to these short pieces as nugae, a Latin word meaning “trifles”, “nuts” or “playful thoughts”.  I invite you to use these ideas as you wish, in any way you find helpful.  I ask only that you kindly cite my writings, which are accompanied by a DOI for proper referencing.

 

Black holes are no longer seen merely as regions of spacetime from which nothing escapes. Over the past decades, developments in quantum gravity and information theory have shown that black holes possess entropy, emit radiation and scramble quantum information at extreme speeds. These insights have transformed black holes into physical systems that actively process information. Yet, existing approaches primarily focus on paradox resolution such as the information loss problem and lack a systematic framework to interpret black holes as computational devices.

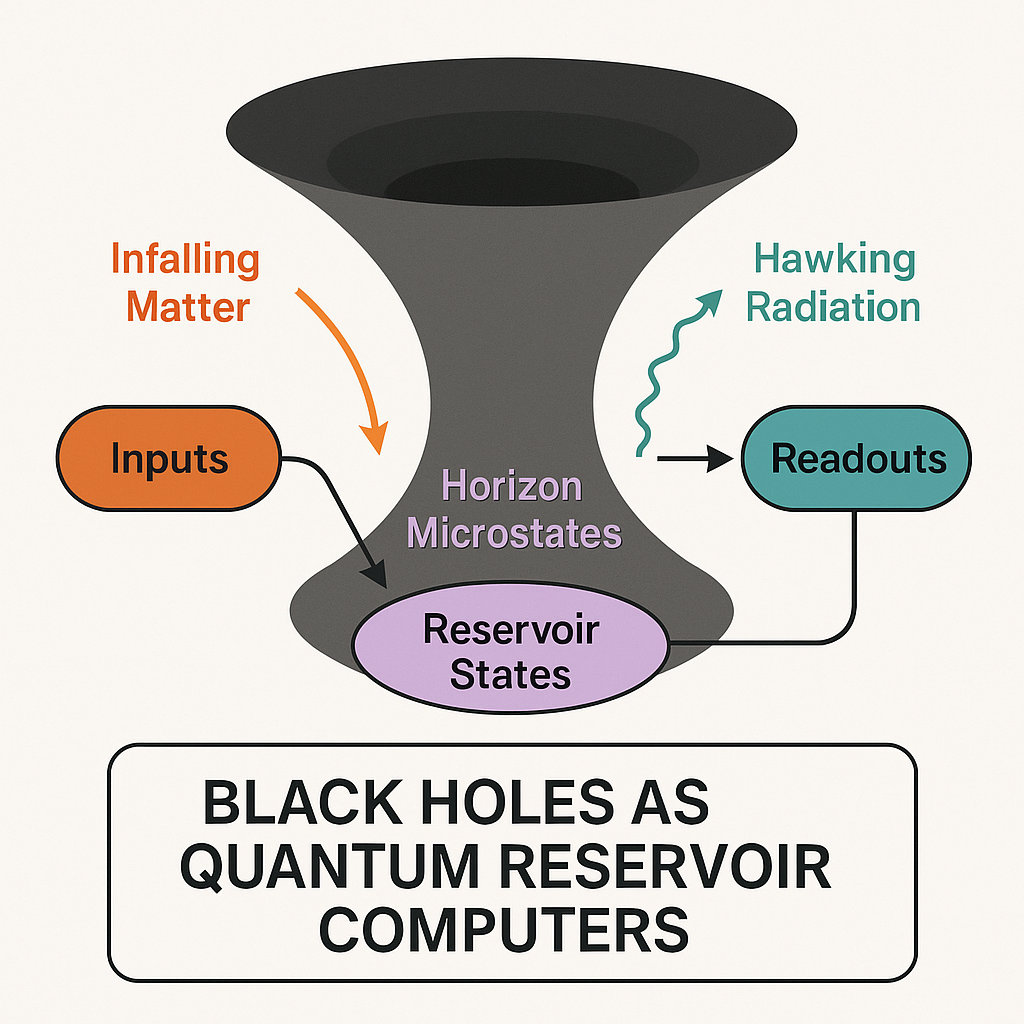
To address this gap, we propose a novel method: modeling black holes as quantum reservoir computers (QRCs). Reservoir computing is a machine learning framework where an input signal is fed into a complex, untrained dynamical system, i.e., the reservoir, which nonlinearly transforms it into a high-dimensional state. A simple, typically linear, readout layer then extracts meaningful outputs. In quantum reservoir computing, this dynamical system is a quantum one, often chaotic, allowing rich temporal encoding and transformation of information with minimal training effort.

We suggest to map this structure onto black holes. Infalling matter or radiation corresponds to the input signal. The black hole’s near-horizon quantum microstates—governed by strongly entangling, chaotic dynamics—form the reservoir. The emitted Hawking radiation or holographic observables serve as the readout layer. This analogy is supported by known black hole properties: their scrambling behavior aligns with the QRC's fading memory (echo state property) and their entropy limits their information capacity, just as a reservoir’s dimensionality bounds its memory and learning power.

Our proposal reframes black holes as natural, untrained quantum systems capable of complex temporal processing. Compared with existing techniques studying black holes purely through thermodynamics or holography, this method provides a computational lens through which to quantify and test memory, scrambling and information flow. It bridges gravitational physics with machine learning and opens a pathway to simulate black hole-like behavior in laboratory quantum systems.

Our perspective enables the formulation of testable hypotheses in analog gravity and quantum simulation platforms. Future research can investigate how different black hole types encode memory, how input signals might be recovered from radiation and whether quantum circuits can mimic black hole reservoirs. Ultimately, this method introduces a new approach for understanding spacetime not just as geometry, but as an active substrate for quantum computation and learning.

 

 

Tozzi A.  2025.  Black Holes as Quantum Reservoir Computers: A New Computational Perspective on Gravity. July 2025. https://doi.org/10.13140/RG.2.2.35145.25443.

 

 

 

 

 

NUGAE – HOW MODULAR BIOLOGICAL SURFACES SELF-ORGANIZE UNDER CONSTRAINTS: THE CASE OF ACHILLEA MILLEFOLIUM

Biological surfaces, from leaves to inflorescences, often appear ordered yet never perfectly crystalline. The balance between regularity and disorder is usually described qualitatively or reduced to broad concepts such as phyllotaxis or developmental modularity. In the case of composite flowers such as Achillea millefolium, the prevailing description is that many florets group into capitula which in turn form corymbs, thereby mimicking a single large flower. While this descriptive framework captures the visual impression, it fails to explain how individual florets interact with one another at the surface level, how their geometrical constraints shape collective arrangement and how these local rules translate into energetic economy and robustness.

Our proposal is to study Achillea capitula as modular surfaces able to self-organize under topological and energetic constraints. Each floret can be regarded as a discrete unit occupying a Voronoi-like territory. Its neighbors are defined through Delaunay triangulation, yielding a contact graph that encodes mechanical and spatial competition. Several parameters can quantify this system. First, the degree distribution of the contact graph tells us how many neighbors each floret maintains; its Shannon entropy measures variability in coordination, distinguishing homogeneous from heterogeneous packing. Second, the hexatic order parameter ∣ψ6∣|\psi_6|∣ψ6​∣ quantifies local six-fold symmetry; values close to one indicate quasi-hexagonal packing in the capitulum interior, while lower values reveal defects or edge irregularities. Third, Voronoi cell areas and their coefficient of variation capture how equitably surface is partitioned among florets, while Voronoi entropy measures inequality in resource allocation. Fourth, nearest-neighbor distances and their distribution reflect mechanical pressure and polydispersity of florets.

Taken together, these parameters could define an “interaction signature” of each capitulum, which we expect to vary with position in the corymb, with light exposure and with environmental stress. A healthy capitulum should exhibit moderate to high ∣ψ6∣, low degree and Voronoi entropy and narrow nearest-neighbor distributions, whereas stressed or shaded ones should show breakdown of order and higher variability.

Compared with existing approaches focusing on large-scale phyllotaxis or visual mimicry, our framework provides quantitative, multi-scale and testable metrics of how modular floral units interact. It bridges geometry, topology and energetics without requiring genetic or biochemical data, thus offering a new layer of analysis complementary to developmental and ecological studies.  This could allow the construction of empirical scaling laws between energy availability, growth constraints and surface organization.

Experimental validation can be pursued through high-resolution imaging of capitula across environmental conditions, automated segmentation of florets and computation of the metrics described. Manipulative experiments, such as selective removal of florets, shading of half-inflorescences or controlled nutrient limitation, should produce predictable shifts: decrease of ∣ψ6∣, increase in Voronoi entropy, broadening of nearest-neighbor distributions.

By understanding how modular surfaces self-organize, we could gain insight into fundamental principles of biological design. For plants, these arrangements may maximize visible surface and pollinator attraction while minimizing construction cost, distributing risk and maintaining robustness against damage. Beyond botany, our approach may apply to other modular systems: epithelial tissues where cells compete for surface, coral polyps forming colonies, bacterial biofilms spreading under spatial constraint. Potential applications range from crop science, where inflorescence packing efficiency correlates with yield and resilience, to biomimetic engineering, where controlled disorder can inspire low-energy materials or photonic structures. Future research may extend these metrics to dynamic imaging, capturing how packing entropy and hexatic order evolve over developmental time.

 

QUOTE AS: Tozzi A.  2025.  nugae -how modular biological surfaces self-organize under constraints: the case of Achillea millefolium.  DOI: 10.13140/RG.2.2.21198.52800

 

 

 

 

NUGAE – TOWARDS BACTERIAL SYNCYTIA: A FRAMEWORK FOR COLLECTIVE METABOLISM?

Experimental approaches to multicellular behavior and bacterial collectives usually emphasize surface interactions, nutrient gradients and community coordination via quorum sensing/extracellular molecules.  We suggest that bacterial assemblies could be better understood as functional syncytia, where bacteria are integrated into shared metabolic/signaling units.  The outer cells could act as the colony’s interface with the environment, absorbing stress, harvesting nutrients and sensing external cues, while the shielded inner cells could rely on buffered collective coupling.  Inner cells, deprived of direct ligand access with the external milieu, could display underused and downregulated membrane receptors.  Their physiology could be shaped by collective coupling: for instance, diffusible metabolites, continuously conveyed through nanotubes, vesicles or extracellular redox mediators, could replace receptor-driven signalling.  Still, inner cells could shift between growth, quiescence or persistence in synchrony with the colony, maintaining viability and genetic continuity. 

An interconnected network is achieved whose collective physiology cannot be reduced to single-cell behavior.  A series of dynamical processes involving dynamic coupling point towards gradients and signals that are distributed across the population.  For instance, electrical oscillations (e.g., potassium fluxes in Bacillus subtilis biofilms) propagate across millimeter scales, synchronizing growth and nutrient uptake between distant regions. These ion waves act as excitable media in which local perturbations propagate as traveling fronts, synchronizing collective activity in a manner analogous to action potentials coordinating responses across tissues.  Metabolic cross-feeding (e.g., alanine cross-feeding in E. coli colonies) provides another form of dynamic coupling: inner cells, often hypoxic, secrete metabolites like alanine or lactate diffusing outward, while outer aerobic cells consume them, generating feedback loops of oscillating nutrient gradients.  Vesicle trafficking and nanotube exchange (especially in Gram-negative bacteria) may introduce stochastic but impactful bursts of communication, where packets of proteins, plasmids or metabolites abruptly alter the state of neighboring cells.  These coupled states may also generate bistability, with colonies toggling between high-growth and low-growth regimes depending on stress levels.  

Altogether, the dynamics of a hypothetical bacterial syncytium could be expected to include oscillations, traveling waves, feedback-stabilized heterogeneity, stochastic bursts of exchange and regime shifts akin to phase transitions.

Compared with existing approaches that model biofilms as networks of communicating individuals, our perspective highlights shielding as a structural principle, explaining why inner populations maintain resilience under stress and how robust oscillations and gradients emerge as system-level properties.  

Experimental validation could be pursued through microfluidic devices that enforce layered architectures, enabling direct observation of periphery-to-core propagation of signals. Fluorescent metabolite sensors could test whether inner cells respond to perturbations indirectly, while genetic knockouts disrupting nanotube or vesicle formation would probe the role of coupling in maintaining inner viability.  It would also be feasible to investigate whether inner cells organize into complex networks characterized by distinctive topologies such as small-world architectures or scale-free distributions.  By grounding the analysis in graph-mediated coupling and Laplacian dynamics, our approach may allow theoretical predictions to complement descriptive accounts of bacterial cooperation.  

Predicted outcomes include measurable delays between outer and inner responses, reduced variance in inner activity under stress and traveling front patterns consistent with theoretical diffusion. A clear expectation is that colonies with intact coupling should buffer inner cells against environmental shocks, whereas decoupled populations would fragment into vulnerable individuals. 

Our approach suggests that antibacterial strategies should not only target metabolic activity, but also disrupt the coupling mechanisms that improve collective resilience. Synthetic biologists might exploit bacterial syncytia to build engineered living materials with distributed sensing and metabolic stability.  Over evolutionary timescales, our framework could provide a blueprint for viewing life as a continuum spanning solitary cells to fully integrated multicellular organisms.  Microfluidic scaffolds could be employed to replicate outer-inner architectures and accelerate in vivo adaptive dynamics, positioning bacterial syncytia as an experimentally accessible midpoint for assessing both diversification and evolution. 

QUOTE AS: Tozzi A. 2025.  Nugae -towards bacterial syncytia: a framework for collective metabolism?  DOI: 10.13140/RG.2.2.15224.92164

 

 

 

 

 

NUGAE - TOPOLOGICAL APPROACHES TO THE EVOLUTION OF SPECIES AND INDIVIDUALS

Many mathematical and conceptual approaches in evolutionary biology have incorporated geometric, relational and topological ideas: think to D’Arcy Thompson’s morphogenetic transformations, René Thom’s catastrophe theory, Rosen’s relational biology, Friston’s Free Energy Principle, Juarrero’s constraint closure, Barad’s agential realism, the Extended Evolutionary Synthesis, Walker and Davies’ informational perspective, Wolfram’s rule-based complexity, etc.  Nevertheless, none of these frameworks provide a complete, explicitly topological general account of natural evolution.

We suggest to recast individuals and species as topological phenomena within a high-dimensional configuration manifold whose coordinates integrate genomic, phenotypic, ecological and developmental variables.  An individual becomes a continuous trajectory maintaining local structural coherence, while a species is a connected component sustained by the turnover of constituent points.  Selection is reformulated as the persistence of topological features under perturbation, extinction as the collapse of these features, reproduction as a cobordism linking trajectories in higher-dimensional spaces, while adaptation as the occupation of regions where compatibility conditions, formalizable in sheaf theory, are satisfied.

The advantage of this formulation lies in replacing fitness and goal-based narratives with persistence of invariants such as Betti numbers and lifetimes of cycles, yielding a unified, scale-independent mathematical description compatible with nonequilibrium thermodynamics and information theory.  Still, it is empirically tractable via persistent homology robust to noise and incomplete data.

Methods to test this topological framework include embedding longitudinal multi-omics, phenotypic and environmental datasets into state spaces, computing Vietoris–Rips or witness complexes, tracking persistent features through time, running controlled microbial evolution experiments with environmental perturbations and simulating rule-based or agent-based models to check whether invariant structures emerge under non-teleological rules.

Testable hypotheses include that speciation corresponds to the birth of new connected components and shifts in Betti-0, that developmental canalization corresponds to stabilization of higher-dimensional cycles across ontogeny, that evolutionary convergence reflects attraction to the same homology class, that persistence lifetimes of invariants outperform classical fitness metrics in predicting lineage survival.  

Potential applications include forecasting evolutionary trajectories from invariant structure, identifying ecological niches as persistent regions in morphospace, detecting early-warning signals of collapse through topological transitions, designing synthetic organisms for structural persistence and building evolutionary algorithms to optimize invariant persistence without teleological accounts.  Future research could develop category-theoretic underpinnings linking constraint closure to sheaf cohomology, relate Markov blanket boundaries to nerve complexes of interaction graphs, derive thermodynamic limits on invariant lifetimes and implement scalable topological data analysis pipelines for eco-evolutionary dynamics.

 

QUOTE AS:  Tozzi A.  2025.  Topological Approaches to the Evolution of Species and Individuals.  DOI: 10.13140/RG.2.2.35506.52163

 

 

 

 

 

NUGAE - WAS IMMUNITY THERE FIRST? A NEW PERSPECTIVE ON LIFE’S ORIGIN

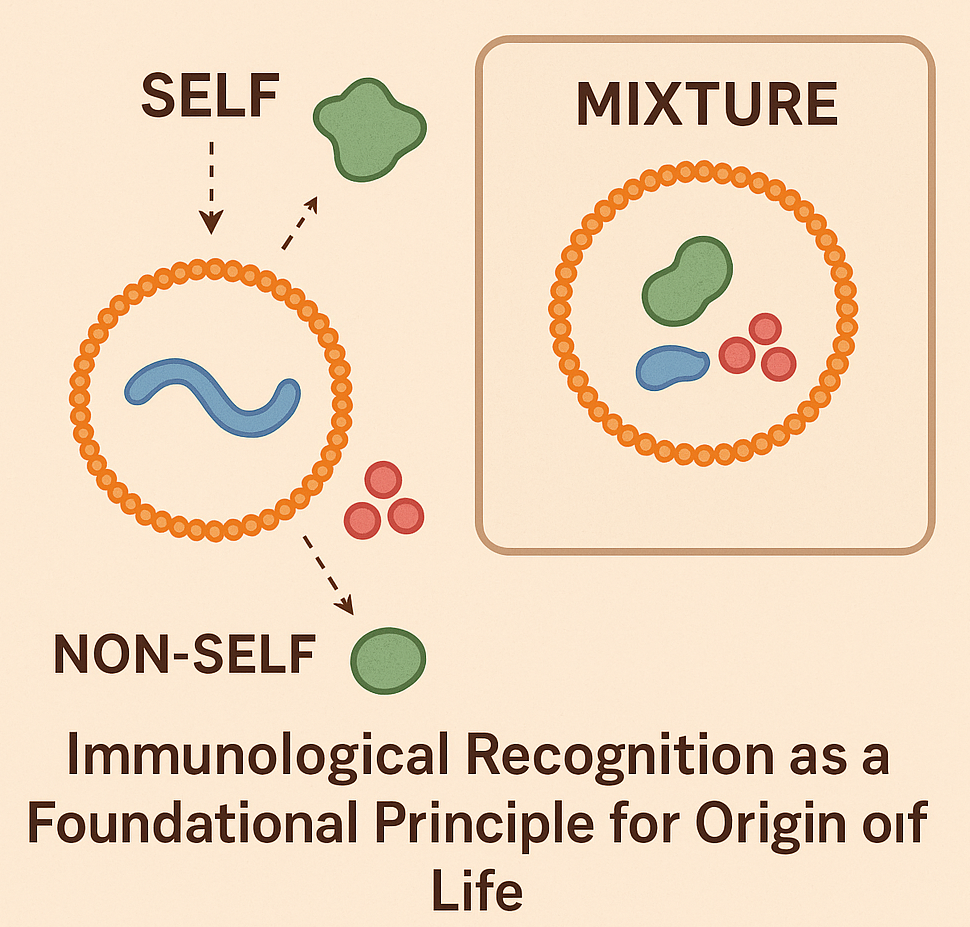
Most prevailing models of the origin of life focus on the formation of self-replicating molecular systems as the key step toward the occurrence of the first cells, emphasizing the role of either metabolism, compartmentalization or replication of RNA and other polymers. Yet most origin-of-life models overlook a fundamental property of all living systems, i.e., the ability to distinguish self from non-self, a core immunological function central to biology.  We propose to integrate the immunological principle of identity maintenance to explore whether primitive forms of molecular recognition were a necessary prerequisite for the emergence of life.  We hypothesize that even the earliest protocells or molecular systems required a minimal capacity to recognize and preserve their own components while excluding or neutralizing harmful elements, as this function would have been essential for achieving stability, accurate replication and long-term persistence.

To experimentally explore the theoretical immunological functions of protocells and reconstruct minimal conditions for self/non-self discrimination, we propose using lipid vesicles as model systems of protocells encapsulating well-defined “self” molecules such as RNA analogs, short peptides or labeled polymers. These protocells would be introduced into environments containing a complex mixture of “non-self” molecules, e.g., synthetic analogs of potentially parasitic or disruptive agents.  By varying the chemical nature, charge and sequence specificity of both self and non-self molecules, we could assess how protocells respond in terms of stability, retention of contents and selective uptake or exclusion.  Molecular crowding agents and environmental stressors (e.g., pH shifts, ionic fluctuations) would simulate potential early Earth environments.  This setup would allow us to test whether physical, chemical or molecular properties (e.g., selective permeability, primitive recognition motifs, molecular competition, binding specificity or environmental noise) may enable protocells to preserve their molecular identity over time.  Fluorescence tagging and microscopy would track the interaction dynamics, while leakage assays and molecular degradation measurements would quantify vesicle integrity and self-preservation.  Additional experiments could incorporate engineered membrane proteins or synthetic receptors to test primitive recognition motifs and mimic early forms of selective binding.  

Overall, we introduce the perspective that life may have required an early form of molecular “recognition” preceding, or occurring alongside, replication.  This perspective may provide insight into how primitive identity mechanisms evolved into complex immune functions and could also guide future studies on molecular discrimination, rise of parasitism and early strategies for coping with environmental stress. 

QUOTE AS: Tozzi A. 2025. Nugae -Was Immunity There First? A New Perspective On Life's Origin.   DOI: 10.13140/RG.2.2.13691.22561

 

 

 

 

 

LACKING RESOURCES AT THE ONSET OF LIFE: USING LINEAR LOGIC TO MODEL HOW LIFE BEGAN

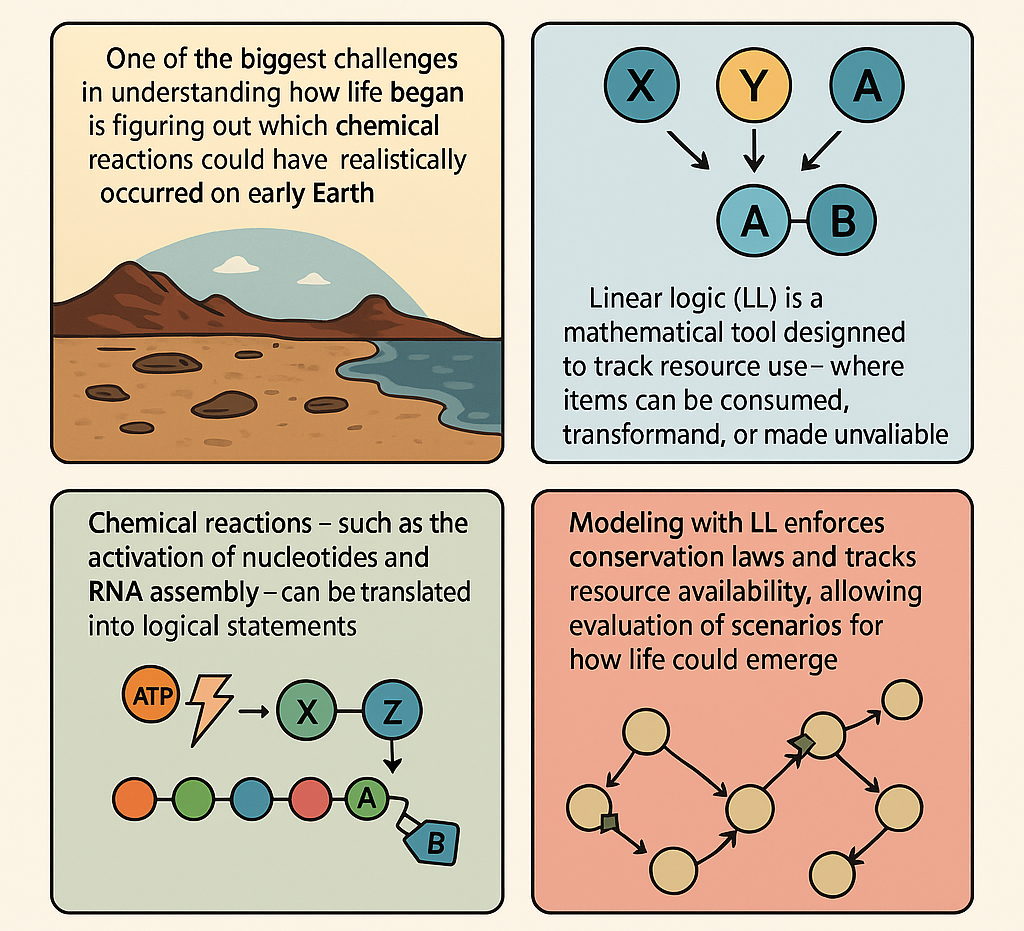
One of the biggest challenges in understanding how life began is figuring out which chemical reactions could have realistically occurred on early Earth. Most models assume that molecules like RNA could self-replicate, but they often don’t take into account how limited resources—like energy or building blocks—might have constrained these processes. To address this, we can use a tool from mathematical logic called Linear Logic (LL), which is designed to track how resources are used and transformed.  Linear Logic is different from ordinary logic. In classical logic, you can reuse assumptions as many times as you like. But real-world chemistry doesn’t work that way. If you use up a molecule in a reaction, it’s gone—you can’t just use it again. LL reflects this principle. It treats every item as something that can be consumed, changed, or made unavailable, which is exactly what happens in chemical reactions. For example, in LL, you can’t use the same unit of energy to fuel multiple reactions at once—just like in real chemistry.

The method works by translating chemical reactions—such as the activation of nucleotides, RNA assembly, and even the transition from RNA to DNA—into logical statements within a LL system. These statements represent how many molecules are available, what is needed for a reaction, and what gets produced. By doing this, one can build a complete logical map of a possible pathway toward life, while keeping track of everything being used along the way.  This LL-based framework doesn't just mimic chemistry, rather it enforces strict rules that mirror conservation laws, making sure nothing comes from nothing.  You can simulate different environmental conditions (like temperature changes or radiation) and see how they affect molecular stability or replication. You can also test what happens when resources are scarce or when catalysts are added. 

In short, this approach offers a formal and testable way to evaluate how life could have emerged from non-living matter. It doesn’t aim to simulate every detail but instead provides a resource-sensitive framework for checking whether a proposed sequence of reactions is even possible. Scientists can use this logic-based method to rule out impossible scenarios, highlight promising ones and ultimately guide experiments that explore the origins of life in a more structured and realistic way.

QUOTE AS:  Tozzi A. 2025. Prebiotic Resource Constraints and the Origin of Life: A Linear Logic Framework.  bioRxiv 2025.03.23.644802; doi: https://doi.org/10.1101/2025.03.23.644802    

 

 

 

 

WHY ORDER MATTERS IN BIOLOGY: A MATHEMATICAL WAY TO UNDERSTAND SEQUENCE-DEPENDENT SYSTEMS

Many biological and evolutionary processes depend not just on what happens, but on the exact order in which things happen. For instance, the order in which transcription factors bind to DNA can decide whether a gene is turned ON or stays OFF. Similarly, in evolution, the sequence in which mutations occur can change the outcome—even if the same mutations are present. This “order sensitivity” makes biological systems non-commutative, meaning reversing steps can lead to different results.  Traditional biological models often ignore or simplify this directionality. To address this, the paper applies a mathematical tool called the Wedderburn–Artin theorem. This theorem helps break down complex non-commutative structures into simpler, manageable pieces called matrix blocks. The authors treat biological events (like binding or mutations) as algebraic operations and construct a custom algebra to represent them. Then, using Wedderburn’s decomposition, they divide this algebra into smaller parts that each represent a unique “behavioral module.”

The method was applied to two scenarios:

1. Gene regulation: The model simulates how the order of transcription factor binding (like A before B or B before A) affects gene expression. It showed that only one order (A → B) strongly activates the gene, while others have little or no effect.
2. Evolutionary mutations: The study modeled different mutation orders (e.g., A → B → C vs. C → B → A) and their effects on trait expression. Again, only one specific order led to full trait development, highlighting how mutation history matters.

In both cases, the algebraic method successfully sorted different sequences into functional categories. It also reduced the complexity of analyzing all possible sequences by grouping them into smaller, interpretable modules.

This mathematical framework doesn’t simulate timing or continuous changes, but it’s powerful for understanding systems where the order of steps is critical. The approach could be used in fields like genetics, systems biology, and synthetic biology to uncover which event orders are essential and which are redundant. In short, this paper shows how tools from abstract algebra can help explain and simplify the logic behind real biological systems—especially when the order of events changes everything.

 

QUOTE AS: Tozzi, Arturo. Applications of Wedderburn's Theorem in Modelling Non-Commutative Biological and Evolutionary Systems. Preprint. Posted April 3, 2025. https://doi.org/10.1101/2025.04.03.647006. 

 

 

 

 

NUGAE - A GAUGE-THEORETIC MODEL OF THE HIERARCHICAL LEVELS OF HUMAN CONCEPTUAL KNOWLEDGE

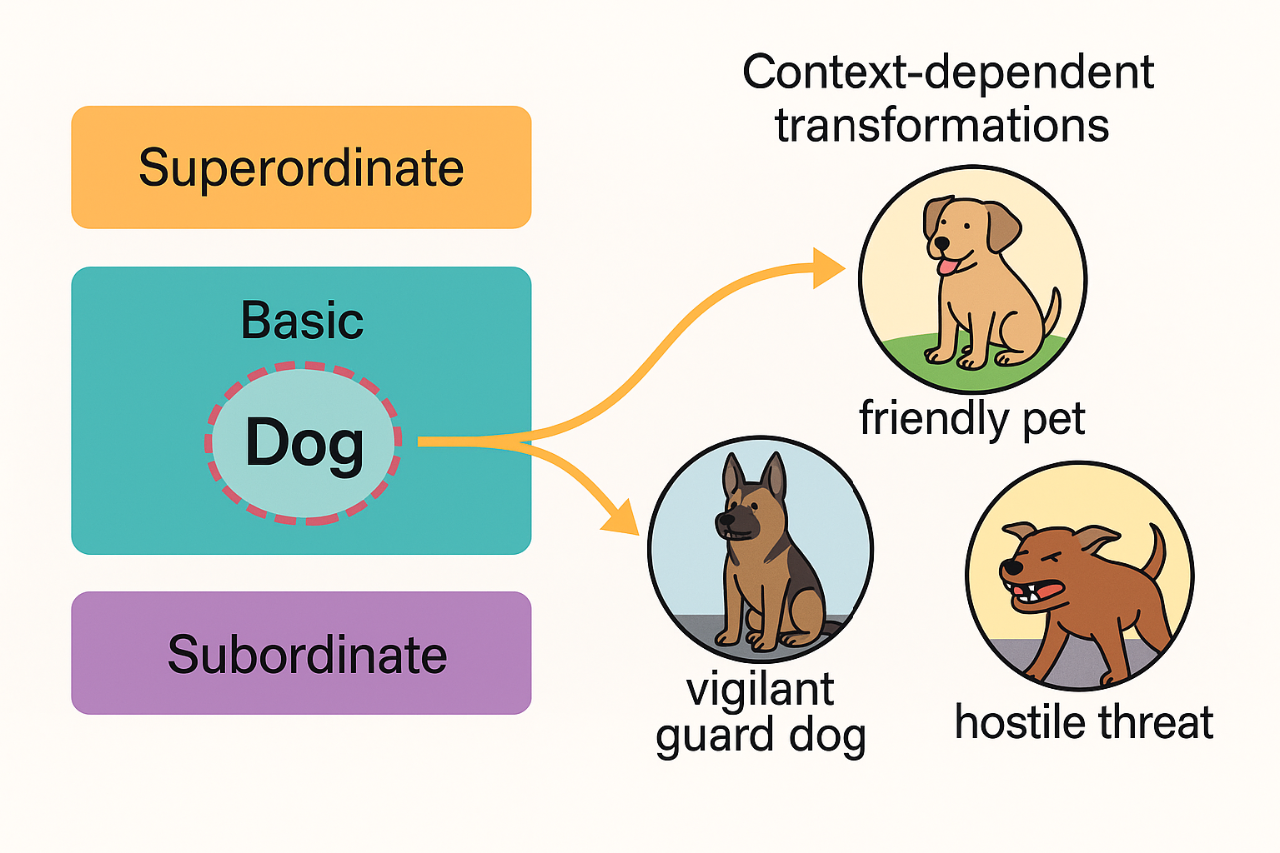
Current theories of conceptual knowledge describe how humans organize ideas at multiple levels, from broad superordinate distinctions like living versus nonliving, to basic categories like animals and down to subordinate distinctions like dog, wolf or beagle. Modern cognitive science shows that people navigate these levels fluidly: they maintain stable category membership while flexibly reshaping the meaning of a concept depending on the situation. However, existing computational models often conflate these levels or fail to capture how meanings shift while the conceptual backbone is kept stable. Neural networks, for instance, can learn fine-grained similarities but struggle to express how context affects the interpretation of the very same item without altering its categorical identity. This reveals a missing mechanism in current models: a way to distinguish the stable structure of conceptual hierarchies from the flexible, contextual interpretation of specific concepts.

Our proposal addresses this gap by adapting a simplified version of gauge theory to conceptual representation. In physics, gauge theories describe systems whose internal configuration can change without altering their fundamental identity, like rotating a compass needle without moving the compass itself. Translating this intuition to cognition, we consider each concept as having two parts.

1. The stable component, which situates it on the semantic hierarchy (dogs are animals, animals are living beings).
2. The flexible component, made of microfeatures whose relevance changes with the context. 

A dog provides a clear illustration. At the hierarchical level, it is always an animal, living and distinct from tools or plants; this position does not change. But the internal meaning shifts dramatically depending on the situation. When adopting a “family-home” frame, a dog is affectionate, familiar and safe. In a “security” frame, it becomes vigilant, strong and protective. Under a “danger” frame, the perceived threat is amplified. These shifts do not modify the concept’s place in the hierarchy; instead, they alter the internal feature weighting. Gauge transformations are used to formalize these context-driven changes. They reorganize the microfeatures without moving the concept from its semantic location, much like reorienting the compass needle without moving the compass.

In our framework, concepts lie on a manifold representing the hierarchical levels, while each concept carries a vector of flexible attributes attached like a small fiber. Contexts act as gauge fields: they apply structured transformations to the fibers, adjusting how the concept is internally represented. This grants a direct way to model how the meaning of a dog changes when one switches from thinking about pets, to thinking about dangerous animals, to thinking about working dogs, all while preserving the stability of the underlying hierarchy.

Compared with embedding-based approaches, our framework clearly separates identity from context, allowing formal control over what changes and what remains fixed. It also predicts structured patterns of semantic deformation: concepts within the same category should shift together under certain contextual frames, while remaining anchored to their hierarchical level. 

This approach suggests several experimental tests. Behavioral similarity judgments should reveal systematic changes in perceived distances between items when the contextual frame is altered. Neuroimaging-based representational similarity analyses should show that coarse-level categories remain stable while fine-grained relations reorganize. Simulations should reveal predictable anisotropies, i.e., greater deformation along certain conceptual dimensions but not others.

Many potential applications can be suggested: modelling conceptual flexibility in language and reasoning, improving AI’s alignment with human conceptual structure, understanding semantic drift and framing effects and studying alterations of conceptual processing in clinical populations. Our approach invites further research into context-sensitive meaning, developmental changes in concept representation and cross-cultural variability in hierarchical organization.

QUOTE AS:  Tozzi A.  2025.  Nugae - a gauge-theoretic model of the hierarchical levels of human conceptual knowledge.  DOI: 10.13140/RG.2.2.30644.10882

 

 

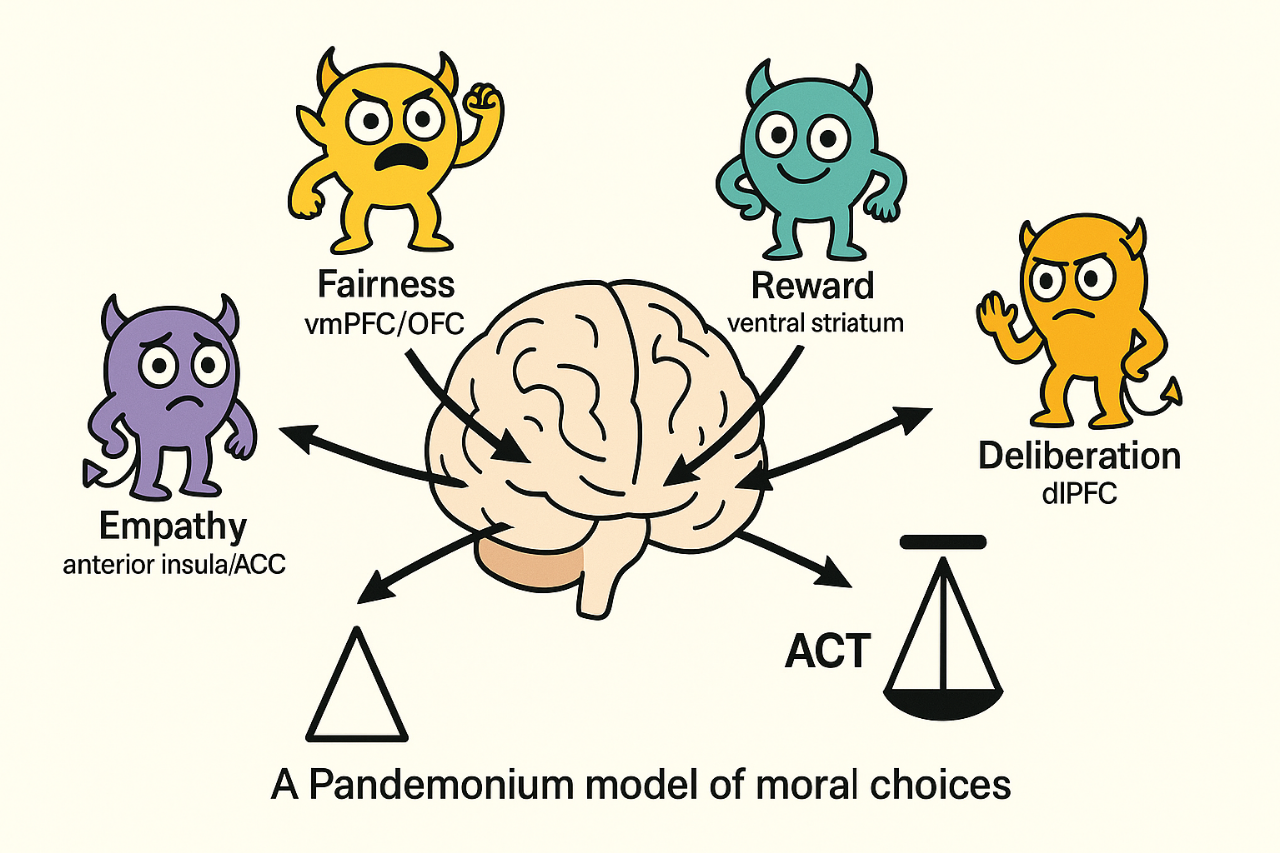
NUGAE - A PANDEMONIUM MODEL OF MORAL CHOICES

Empirical studies increasingly show that moral decision-making arises from distributed and partially independent neural systems whose activity patterns vary dynamically with context. Rather than assuming a central moral faculty or hierarchical control, we propose a Pandemonium model in which moral judgment results from the real-time competition and cooperation among multiple neural subnetworks. Each subnetwork operates as a computational demon, evaluating the same perceptual and contextual inputs under its own objective function. The outcome of this collective dynamic is not a predetermined rule, but rather an emergent equilibrium reflecting the transient dominance of specific evaluative dimensions.    The paper contains some mathematical formulas that are difficult to reproduce in this context. Therefore, you can find here a Word version of the article

QUOTE AS: Tozzi A.  Oct 2025.  Nugae - A Pandemonium Model of Moral Choices.  viXra:2510.0033

 

 

 

 

 

NUGAE - QUALIA MAPPED ONTO MULTIDIMENSIONAL MANIFOLDS OF POSSIBLE AND PROBABLE STATES

The study of qualia has long been caught between two poles: descriptive phenomenology, which stresses the richness and irreducibility of subjective experience and reductive science, which seeks to capture experience through objective correlates such as wavelengths, decibels or neural activations. Both approaches face limits: what is lacking is a framework preserving the open-ended differentiability of qualia while also allowing for tractable representation.

We suggest treating qualia as points and trajectories on a multidimensional manifold, in which every potential axis corresponds to a possible distinction that experience could make salient, e.g., hue, brightness, texture, emotional valence, bodily resonance, temporal unfolding and so forth.  Rather than collapsing experience into a single category, we aim to expand it into a geometric space where fine-grained differences can be located and compared.  

Crucially, we distinguish between possible distinctions, i.e., the full phase space of the discriminations that the perceptual and cognitive system could in principle support, and probable distinctions, which are the actually realized, ecologically weighted and historically constrained differentiations employed by subjects.  The manifold provides the scaffold, while probability distributions assign density to its regions, indicating where distinctions are more likely to occur. In this way, qualia are represented not as fixed states but as probabilistically weighted trajectories through a high-dimensional experiential landscape.  Our formulation provides advantages over existing models of perceptual or affective space, which either focus narrowly on one modality or assume fixed coordinate systems.

Experimental tests could involve psychophysical paradigms where subjects discriminate finely graded stimuli, combined with neural population analyses to assess manifold structures in brain activity.  Topological data analysis, diffusion maps and embedding techniques could approximate the geometry of possible distinctions, while behavioral frequencies and neural likelihoods could estimate the distribution of probable distinctions.  Testable predictions include the emergence of invariant attractors corresponding to recurrent qualia categories and measurable differences between the geometry of possible perceptual spaces and the densities of probable usage.

Our approach may lead to new strategies for interpreting perceptual plasticity and for diagnosing disorders where the weighting of distinctions is altered.  Still, it may inspire artificial intelligence architectures balancing open-ended representational capacity with probabilistic efficiency.  In philosophy, the intractability of qualia could be reframed not as a dead-end, but rather as a structured manifold awaiting exploration.  Future research could extend our framework to collective qualia spaces, intersubjective resonance, multidimensional cues and cross-species comparison, deepening our grasp of how worlds of experience are constituted. 

It would also be possible to use the same language to describe what a bat, a lion or a human perceives.

QUOTE AS: Tozzi A.  2025.  Nugae -qualia mapped onto multidimensional manifolds of possible and probable states. DOI: 10.13140/RG.2.2.23426.75205

 

 

 

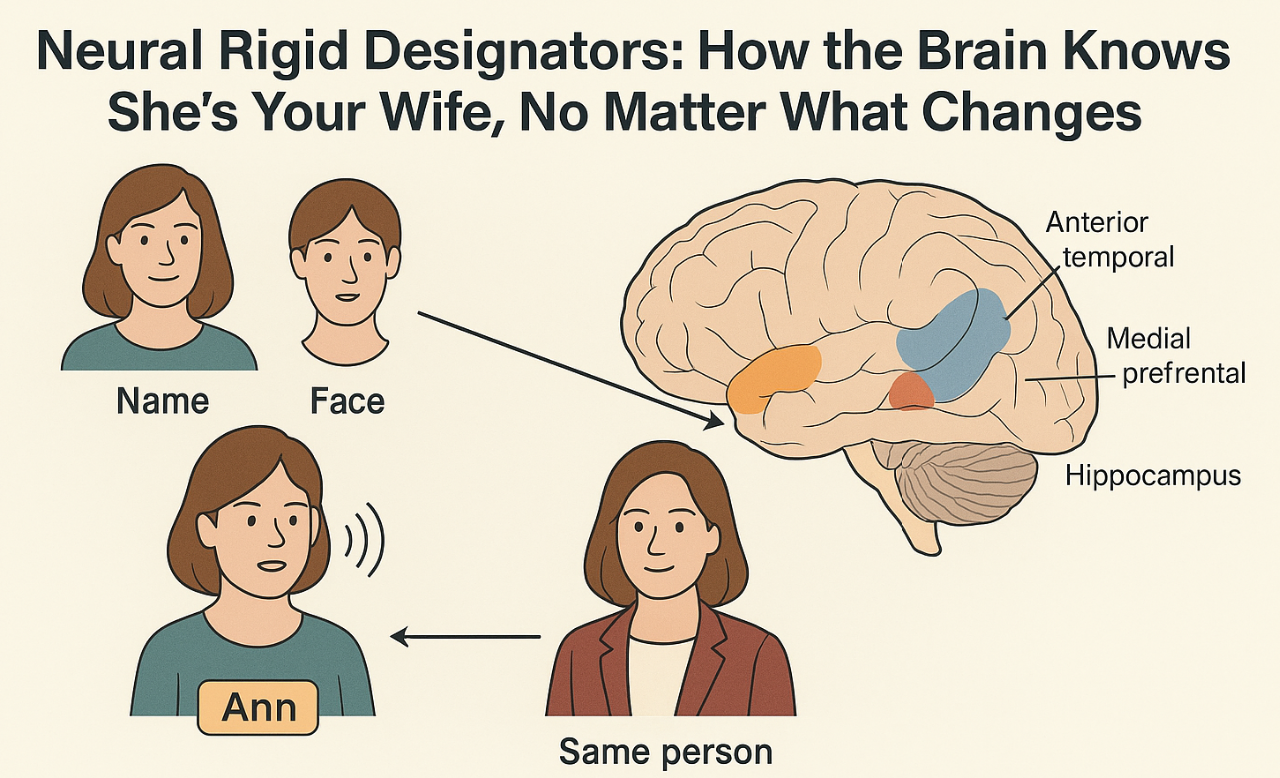
NUGAE - NEURAL RIGID DESIGNATORS: HOW THE BRAIN RECOGNIZES YOUR WIFE, NO MATTER THE CHANGES

The brain recognizes the same person or object across large changes in appearance, viewpoint, sound and context.  Current neuroscientific accounts usually treat identity representations as rich bundles of features or as similarity patterns in a high-dimensional space.  What is still lacking is a bridge between the neural code that fixes an entity’s unique identity (its “who”) and the distinct codes that capture its “what,” namely the features, roles and properties that can change over time or across contexts.

Building on Kripke’s philosophical account, we propose that identity coding in the brain can be understood as a neural rigid designator, i.e., an internal mechanism consistently referring to the same entity across all situations.  It may operate as a stable pointer established at the time of learning and reactivated whenever that entity is encountered, irrespective of changes in its descriptive features. Functionally, it may behave like a label attached to a latent binding slot that persists across time and contexts.  The hippocampus may anchor it to episodic traces, the anterior temporal hub may connect it to semantic attributes and medial prefrontal circuits may regulate its selection according to context and goals.  

Proper names, faces, voices, and symbolic cues can all trigger the same underlying code, which then acts as a key, granting access to information about the individual stored elsewhere in the brain and adapted to the current task. Crucially, this code might remain stable even when surface features (like lighting, hairstyle, social role, etc) change, much like a permanent entry in a mental index that ensures recognition regardless of appearance or circumstance.

Compared with feature-centric or similarity-only approaches, our neural rigid designator could separate reference from description; explain robust cross-modal linking between names, faces and voices; account for dissociations where people lose proper names while retaining descriptive knowledge; support long-range generalization in new settings. 

Methods to test this account could employ representational similarity and encoding models with fMRI and MEG to track identity codes across variations in features and tasks; use cross-decoding to link names with faces or voices; measure repetition suppression as evidence of code reuse; apply causal interference through TMS or intracranial stimulation targeting anterior temporal and hippocampal regions.

Testable hypotheses can be drawn from our hypothesis: identity codes might remain linearly decodable across major changes in surface features; disrupting anterior temporal or hippocampal function might weaken their persistence, while leaving property recognition intact; proper name cues might reinstate the same code activated by perceptual cues; counterfactual alterations of features might not compromise their stability. 

Theoretical applications include: biomarkers for prosopagnosia and semantic dementia; memory-supportive brain computer interfaces; human-robot systems keeping person identity consistent across modalities; AI architectures with entity pointers for co-reference and lifelong learning.  Future research could map developmental emergence, plasticity after injury, interference limits as the number of identities grows and extension from concrete individuals to abstract entities like institutions or theories.

 

QUOTE AS:   Tozzi A.  2025.  Nugae - Neural rigid designators: how the brain recognizes your wife, no matter the changes

doi: 10.13140/rg.2.2.34051.62249

 

 

 

 

 

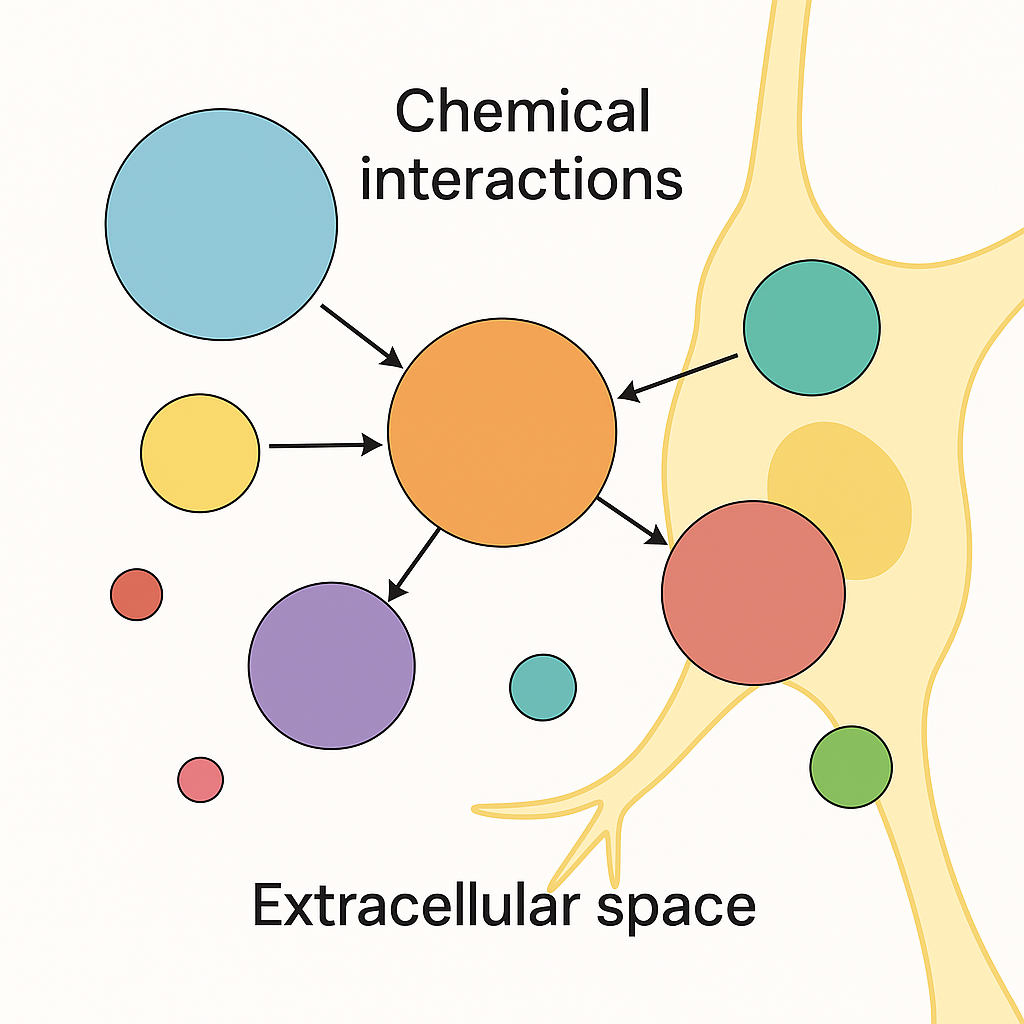
NUGAE - TOWARD A CHEMICAL CONNECTOME OF THE BRAIN’S EXTRACELLULAR SPACE

In neurobiological models, chemical signaling is usually described as a set of linear or localized interactions between neurotransmitters and their receptors. While these approaches capture aspects of fast synaptic transmission and receptor binding specificity, they fail to account for the dynamic complexity of the extracellular chemical environment in the brain. This includes the coexistence and mutual modulation of neurotransmitters, neuromodulators, hormones, peptides, neurosteroids and ions within the perineuronal space. Still, connectome frameworks describe physical or functional connectivity but overlook the biochemical layer where molecules diffuse, interact nonlinearly and influence neural dynamics beyond the synaptic borders.

We propose a framework to conceptualize chemical signaling layer as a high-order network composed of interacting molecular species.  Each chemical messenger may be modeled as a node and the edges may represent regulatory, modulatory or competitive influences (including, e.g., enzymatic degradation, transporter competition, receptor cross-talk and co-release).  Higher-order connections may capture convergence on common second messenger systems, feedback loops within endocrine-neural circuits and shared structural modulators like the extracellular matrix.  A chemical connectome may account for time-dependent features like circadian hormone release, activity-dependent diffusion and stress-responsive neurochemical shifts, all embedded in a spatially defined topology reflecting region-specific receptor expression and extracellular gradients. Our approach could represent emergent properties of brain chemistry such as redundancy, buffering, antagonism, synergy and temporal gating, phenomena poorly captured by pairwise or purely anatomical connectomes.

To test experimentally our hypothesis, one could employ multi-modal molecular imaging, genetically encoded neurotransmitter sensors and real-time microdialysis in combination with optogenetics or pharmacological perturbation to monitor how changes in one messenger affect the spatial distribution and activity of others.  Testable hypotheses include whether elevation of one transmitter (e.g., dopamine) dynamically alters extracellular half-lives or receptor availability of others (e.g., serotonin or glutamate) or whether co-released peptides (e.g., NPY) extend or buffer classical neurotransmission.  Applications range from simulating drug interactions to elucidating neurochemical mechanisms of psychiatric disorders, in which dysfunction may arise from widespread network-level imbalances rather than isolated receptor abnormalities. In neuroengineering, our approach could inform artificial neuromodulatory control in brain-computer interfaces.

Future research may explore how high-order chemical networks interface with structural and functional networks in the brain, forming a multi-layered chemical connectome that encompasses molecular interactions.  Practical examples include serotonin inhibiting glutamate release presynaptically, dopamine and serotonin competing for monoamine oxidase degradation or neurosteroids like allopregnanolone enhancing GABAergic inhibition via allosteric modulation.

Overall, the extracellular space may stand for a computational milieu where chemical signals do not simply coexist but actively constrain and enable one another’s functions.

QUOTE AS: Tozzi A.  2025.   Nugae -toward a chemical connectome of the brain's extracellular space.  DOI: 10.13140/RG.2.2.22042.15046.

 

 

 

 

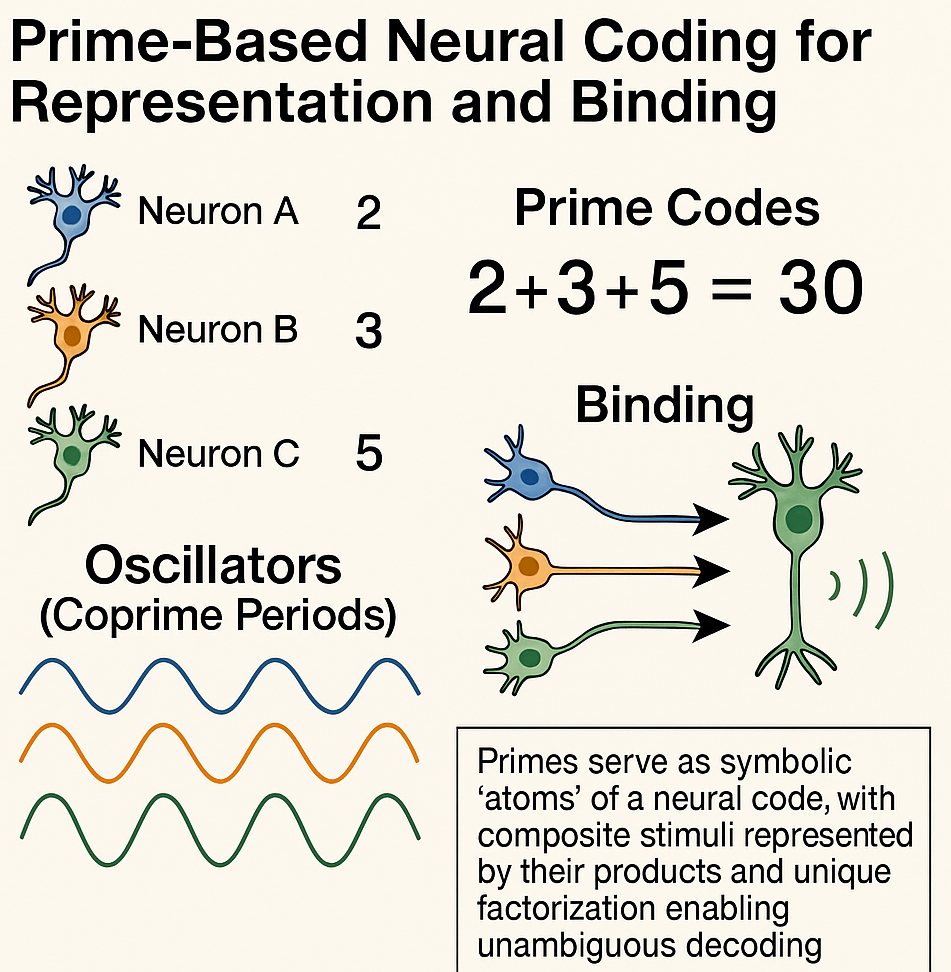
NUGAE - MODELS OF NEURAL REPRESENTATION AND BINDING BASED ON PRIME NUMBERS

Neuroscience has long sought efficient and unambiguous coding schemes to assess how neural systems represent, bind and multiplex information.  Various current models rely on spike timing, rate codes, oscillatory phase coding and population vector approaches, which successfully capture several aspects of neural computation but often struggle with the huge amount of possibilities, the binding problem, etc.

Prime number theory may provide a mathematical alternative: primes could be used as indivisible symbolic atoms for neural codes, leveraging the unique factorization theorem to guarantee that any combination of features can be represented by a single composite number and decoded without ambiguity. Each neuron, feature or informational unit could be assigned a prime: simultaneous activation corresponds to multiplication of their assigned primes, while decoding simply requires factorization. This leads to a biologically plausible implementation by mapping primes to residues in oscillators whose cycle lengths are coprime.  This would enable Chinese Remainder Theorem–based phase code that the brain could implement through well-known oscillatory microcircuits like theta–gamma coupling (see the CODA for more technical details).

Compared to existing approaches, our prime numbers approach to brain computations provides built-in noise robustness, since small perturbations in spike timing or phase cannot alter the factorization unless the disturbance is extreme.  The model scales efficiently, as a small set of primes can encode vast combinatorial repertoires and allows multiplexing of independent streams without interference.

Experimentally, the model could be tested by training spiking networks or neuromorphic circuits with oscillators set to coprime periods and teaching them to represent feature combinations, then measuring decoding accuracy and resilience to noise. In vivo, one could look for task-dependent oscillatory components with coprime periods and phase signatures corresponding to learned feature conjunctions. Testable hypotheses include: during tasks requiring complex binding, narrowband oscillations will emerge at coprime-related frequencies; lesions to specific oscillators will cause predictable “arithmetic” decoding errors; specific combinations of features will yield rare cross-frequency alignment events corresponding to the least common multiple of their assigned periods.

Potential applications span from improving artificial neural networks’ ability to bind and unbind features, to brain–computer interface encoding schemes, to error-resilient communication protocols inspired by neural computation. Future research could explore adaptive prime assignment through synaptic plasticity, hybrid architectures combining number-theoretic representations with probabilistic inference and integration of prime-based codes with rate and temporal codes.

 

CODA.  Biologically-plausible neural architectures exploiting prime factorization could be built by assigning each informational feature (e.g., a neuron, or a microcolumn, etc.) a unique prime-based code.  A small set of neural oscillators, each with a cycle length corresponding to a pairwise coprime or prime number, would serve as a temporal scaffold. When a feature is activated, it induces precise phase shifts in each oscillator according to its assigned residues.  When multiple features are active, these phase shifts sum, performing multiplicative binding through the Chinese Remainder Theorem. Phase-selective neurons would then decode the residue pattern from the oscillators and an associative microcircuit could reconstruct the original feature set. Rare alignments of all oscillators, corresponding to the least common multiple of their periods, would signal specific conjunctions, creating a natural detection mechanism for complex bindings. Learning of the prime-residue mapping could occur through spike-timing-dependent plasticity, while neuromodulatory signals would control whether the network operates in a write or read mode. Overall, this theoretical architecture would provide a compact, noise-resilient and combinatorially rich coding system, potentially allowing the brain to represent vast numbers of feature combinations with minimal resources. 

QUOTE AS: Tozzi A.  2025.  Nugae -models of neural representation and binding based on prime numbers.  DOI: 10.13140/RG.2.2.32082.26562

 

 

 

 

 

COULD DENDRITIC SPINE ARCHITECTURE SHAPE A TOPOLOGICAL LANDSCAPE FOR MEMORY STORAGE AND RETRIEVAL?

We hypothesize that memory may emerge from the spatial arrangement of countless dendritic spines across neurons, giving rise to a topological landscape that supports distributed, resilient and overlapping encoding/retrieval across neural networks. 

Memory storage involves synaptic plasticity, i.e., changes in synaptic strength and number, driven largely by the remodelling of dendritic spines.  Long-Term Potentiation, AMPA receptor trafficking and spine clustering are core mechanisms in this model.  Nevertheless, these explanations remain local and linear, assuming memory is encoded at specific sites and strengthened through repetition. While useful for describing short-term and mechanistic changes, they fall short in accounting for how memory is distributed, redundant, resilient and capable of flexible association and recall..

We hypothesize that memory is not stored at isolated synapses or confined to discrete neural units.  We propose that the spatial arrangement of countless dendritic spines across neurons gives rise to a high-dimensional, transient topological manifold, in which each spine represents a spatial coordinate within that structure. Dendritic spines may serve not merely as passive recipients of synaptic input, but as active, spatially positioned nodes in a continuously evolving encoding landscape.  Their patterns of spatial proximity, morphology and coordinated timing of activation may form a flexible field through which memory traces emerge, interact and persist.  

Our framework suggests that memory traces may emerge as diffuse, resilient network-wide constructs, interwoven with other traces.  One key implication is that even partial patterns (subsets of spine clusters or activity waves) could be useful to reconstruct the full or approximate content of a memory. This aligns with observations in cognitive neuroscience, where memory recall can be triggered by fragmentary cues or partial reactivation.  Also, it may explain how overlapping memories can coexist without overwriting one another, and how degraded or noisy signals can still yield meaningful retrieval.  Still, our topological account of the dendritic spine manifold defines memory as a spatially organized, emergent process, potentially explaining how memories can be redundant, overlapping, associatively linked, and both resilient and adaptable over time.  

To experimentally investigate our hypothesis, one could use two-photon imaging to track spine growth, decay and clustering during learning tasks.  Cell tagging with optogenetics would allow researchers to link specific spine patterns to memory traces.  High-resolution 3D electron microscopy reconstructions could analyze the geometry of spine distributions, while computational modeling might simulate spine interference fields using wave-based algorithms.

To uncover hidden geometric patterns in memory-related spine arrangements across time and neuronal populations, topological techniques such as persistent homology, simplicial complexes and manifold learning (e.g., UMAP, t-SNE) can be applied.  These methods may enable analysis of the shape, connectivity, clustering and high-dimensional structure of evolving dendritic spine distributions.

In artificial intelligence, our model may inspire biologically grounded memory architectures that rely on spatial pattern encoding rather than rigid storage units. In neuroscience, it may reframe neurodegeneration not as the loss of individual synapses, but as the disruption of coherent spatial patterns, potentially enabling earlier and more targeted diagnostics. Clinically, it opens the door to interventions for trauma and memory disorders by aiming to restore or reinforce disrupted spatial memory structures. 

 

QUOTE AS:  Tozzi A.  2025.  Nugae -Could Dendritic Spine Architecture Shape A Topological Landscape For Memory Storage And Retrieval?  DOI: 10.13140/RG.2.2.34279.36002

 

 

  

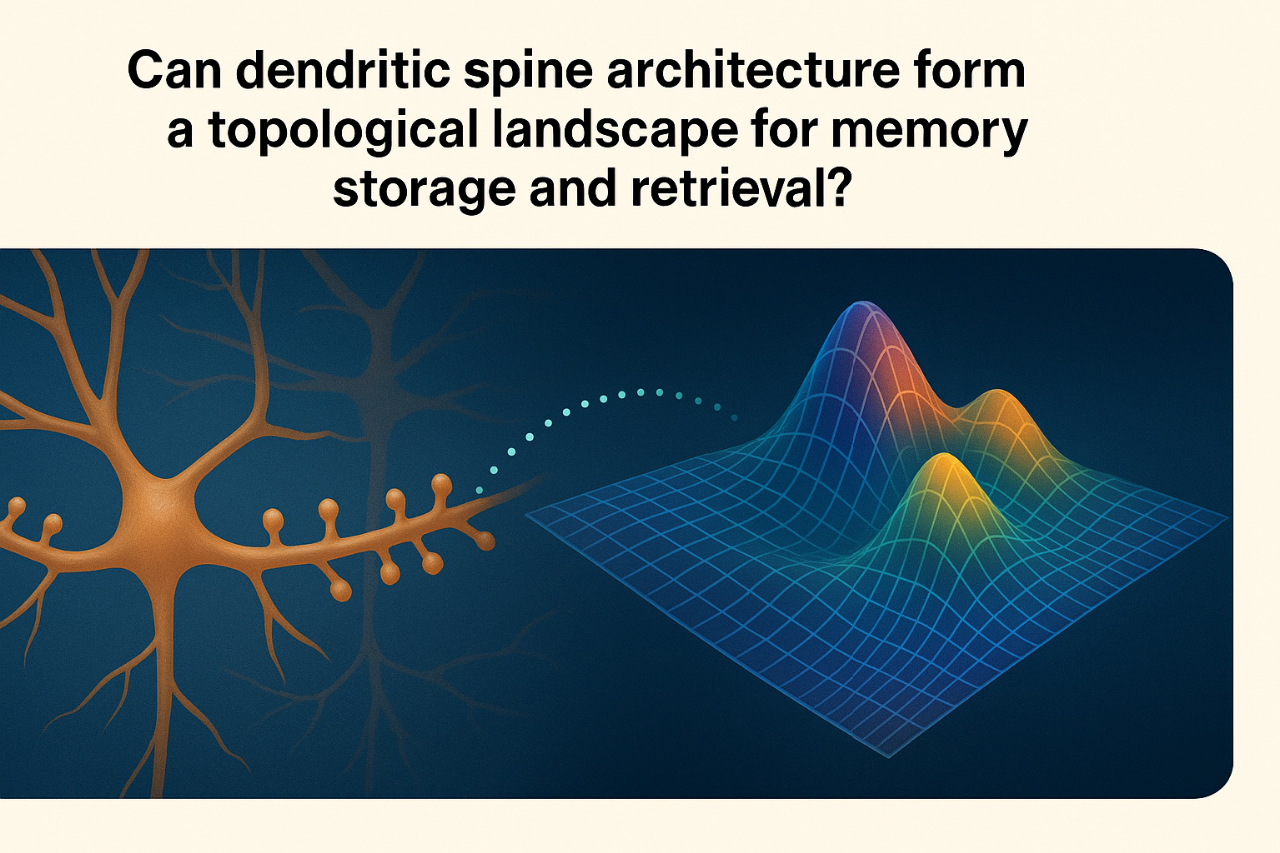
NUGAE - WHEN ANTIBIOTICS STOP WORKING: TOWARD DRUG-FREE POULTRY SYSTEMS?

A large multicenter trial recently published in NEJM (2025) examined whether mass administration of azithromycin to infants in Mali could reduce mortality or infectious disease incidence.  The result was negative: no significant differences were found between azithromycin and placebo groups. This finding could challenge a long-held assumption in both medicine and agriculture, i.e., that broad, preventive antibiotic exposure is intrinsically beneficial. For decades, the success of antibiotics in treating acute infections justified their prophylactic use in large populations, including livestock.  The NEJM null result would, paradoxically, serve as a model of health without intervention, a warning that the time has come to abandon prophylactic antibiotics altogether.

Experimental validation could involve controlled poultry studies where macrolide use is completely suspended, monitoring infection rates, productivity, and microbiome structure over several generations. If outcomes remain stable or improve, this would confirm that antibiotic withdrawal restores resilience rather than inviting disease. Predictably, one should observe transient microbiome fluctuations followed by a re-emergence of balanced commensal populations and decreased antibiotic-resistance gene prevalence.

An antibiotic-free approach to poultry, if validated, has clear advantages over existing approaches focused on developing new antimicrobial compounds or rotating drug classes. Instead of escalating the biochemical arms race, it reframes antibiotic policy as an ecological optimization problem. The benefit lies not in invention but in withdrawal, letting microbial communities regain their adaptive coherence while reducing resistance pressure across ecosystems.

Beyond poultry, this shift heralds a broader transformation in health management. It invites a future where biological stability replaces chemical control, where we learn to cooperate with microbial ecosystems rather than suppress them. The implications reach from agriculture to neonatal medicine, from antibiotic stewardship to microbiome engineering. The failure of azithromycin to confer additional benefit may not mark the end of antibiotics, but the beginning of a world mature enough to live without them.

 

 

 

 

NUGAE - PANDEMONIUM WARFARE: MODELING TUMORS AS BATTLING CELLULAR ARMIES

Current tumor modeling approaches either treat tumors as homogeneous masses or focus solely on their genetic features. These reductionist frameworks fall short in explaining how tumors behave over time, particularly in the face of selective pressures like immune surveillance or therapy.  They ignore the spatial and temporal complexity of the tumor microenvironment, i.e., the arena where different cellular factions interact, compete and adapt. As a result, we lack the tools to understand and predict why some potentially dangerous cells are eliminated while others escape detection and proliferate.  As recent studies have shown, cancer is not simply characterized by uncontrolled cell growth, rather is the outcome of ongoing competition between different cell populations within the body. Far from being passive victims of malignant transformation, healthy cells can detect and actively eliminate their dysfunctional neighbors through cell competition.  Such quality-control mechanism, long studied in developmental biology, involves healthy cells identifying and outcompeting cells that are genetically or metabolically abnormal.  Internal cellular conflicts play a significant role in maintaining tissue integrity and eliminating potentially precancerous cells before they establish dominance. Cells can push out, kill, or even cannibalize their defective counterparts, creating a hidden battlefield that influences also the early stages of cancer development.

Given these premises, we propose a conceptual and computational framework inspired by Selfridge’s Pandemonium architecture. Originally designed to assess how perception emerges from competition among autonomous “demons,” in our adaptation each “demon” is not a feature detector, but a biological agent, such as tumor subclones, immune cells, stromal components, signaling pathways.  These agents act independently, sensing their local environment and “shouting” based on their internal activation levels. Their competition determines which cell types or behaviors become dominant within the tumor at a given time. 

This idea could be implemented by employing agent-based modeling, a simulation technique well-suited to systems composed of interacting individuals with variable behaviors. Each agent (or demon) may be defined by specific traits: proliferation rate, resistance to stress, responsiveness to immune signals or metabolic needs.  Still, each agent may detect environmental cues (e.g., nutrient availability, drug concentration, oxygen levels) and adjusts its activity accordingly.  Then, agents may compete for dominance within discrete microenvironments. The “loudest” agents, i.e., those most strongly activated, shape the local behavior of the tumor, determining whether it grows, regresses or mutates.

Unlike top-down or equation-based models, our decentralized architecture permits emergent behavior. Cells don’t follow a predetermined script.  Instead, their behavior arises from their local interactions and environmental context, mirroring the chaotic but structured nature of real tumor progression.  Moreover, the modular nature of our model allows for expansion: new agents can be added to simulate specific immune cells, therapies or even evolving tumor phenotypes without rewriting the entire system.  The advantages of our approach are manifold. First, it captures both intra- and inter-clonal competition, reflecting the ecological dynamics within the tumor microenvironment. Second, it allows for realistic complexity, showing how multiple forces (e.g., hypoxia, drug pressure, immune infiltration) interact to shape tumor evolution. Third, it has predictive power: the model can simulate how interventions like drug treatment or immunotherapy might shift the competitive balance within the tumor, potentially forecasting resistance or relapse. Finally, our approach is mechanistically informative: by tuning parameters or altering environmental conditions, researchers can explore why some interventions fail and identify leverage points where the competitive landscape could be tilted in favor of healthy or therapeutic agents.

Our model also generates testable experimental hypotheses. For example, would enhancing the “voice” of normal epithelial cells in early lesions reduce tumor incidence? Could environmental modulation like increasing oxygen or decreasing glucose change the outcome of clonal competition? Might the introduction of low-dose therapies at early stages shift dominance away from aggressive clones without selecting for resistance?  Our architecture could be extended by incorporating real-world data (e.g., single-cell transcriptomics or patient-specific mutation profiles) to customize simulations and guide personalized therapy planning.  It could also be applied to model tumor–immune dynamics by adding immune “demons” that sense abnormal cell activity and compete to neutralize it. Similarly, the model could be adapted to assess metastasis by simulating competition between local tumor cells and metastatic seeding cells entering new environments. 

Overall, by drawing from cognitive science to model cellular competition, we propose a new way to conceptualize tumors, not as uniform masses, but as battlefields of competing cellular factions.  Our Pandemonium-inspired framework may provide a richer understanding of tumor ecology and open the door to more adaptive, strategic interventions in cancer treatment.

 

QUOTE AS: Tozzi A.  2025.  Nugae -Pandemonium Warfare: Modeling Tumors As Battling Cellular Armies.  DOI: 10.13140/RG.2.2.35698.21444

 

 

HARNESSING CORIOLIS-SENSITIVE MIGRATION IN MOSQUITOES TO IMPROVE MALARIA PREVENTION TIMING

Current malaria control strategies focus on localized vector suppression, but face major limitations: they often fail to address the long-range seasonal migration of Anopheles mosquitoes. Traditional assumptions held that mosquitoes travel only short distances. However, new findings show that gravid females can migrate hundreds of kilometers at high altitudes, riding wind currents between regions of seasonal rainfall. These migration patterns help explain how mosquito populations suddenly surge at the onset of wet seasons in areas that previously had none during the dry season.

One major limitation in current prevention approaches is the failure to account for these long-distance migrations, which can repopulate regions even after successful local vector elimination. Moreover, these migrations may help spread insecticide-resistant mosquito populations or drug-resistant parasites across vast areas, undermining regional efforts at disease control.

To address this, we propose a novel hypothesis: that mosquitoes may use their halteres (flight-stabilizing sensory organs) to detect Coriolis forces near the equator and navigate across hemispheres in search of wet breeding grounds. This concept leverages the topologically robust nature of equatorial airflows — such as Kelvin and Yanai waves — which arise from Earth’s rotation and break time-reversal symmetry, potentially providing stable migratory corridors. Unlike random windborne dispersal, this model suggests a biologically tuned, directionally sensitive mechanism driving equatorial mosquito migration.  This hypothesis opens new avenues for malaria prevention. For instance, if mosquitoes consistently migrate across the equator before regional wet seasons, timing the administration of short-lived interventions — such as monoclonal antibodies — just before these migrations could significantly disrupt transmission. Specifically, applying these strategies during February–March in the Northern Hemisphere and September–October in the Southern Hemisphere could align with anticipated mosquito influxes.

Compared to conventional vector control, this method targets predictable large-scale movements rather than reacting to local outbreaks. It aligns with emerging findings in atmospheric science, entomology, and disease modeling. Potential applications include integrating this understanding into climate-driven forecasting models, gene-drive strategies, or aerial surveillance systems.  Future research should investigate whether mosquitoes actively detect Coriolis-induced cues via their halteres, possibly through lab-based behavioral experiments or field tracking with scented markers or genetic tagging. A key hypothesis to test is whether migration patterns correlate with equatorial Coriolis dynamics and whether disrupting this navigational cue impairs long-range flight. Confirming such mechanisms could revolutionize our understanding of vector ecology and optimize seasonal malaria control efforts across hemispheres.

QUOTE AS: Tozzi A. Anopheles' peri-equatorial migration via Coriolis forces (electronic response to: Wu RL, Idris AH, Berkowitz NM, Happe M, Gaudinski MR, et al.  2022.  Low-Dose Subcutaneous or Intravenous Monoclonal Antibody to Prevent Malaria.  N Engl J Med 2022; 387:397-407. DOI: 10.1056/NEJMoa2203067).  How do mosquitoes survive during the dry African seasons?

 

 

 

 

THE HIDDEN DIMENSIONS OF REALITY

Most of us grow up thinking the world is made of things: atoms, cells, organisms, planets, brains, tables, cats. But there is another way to think about reality, one that scientists increasingly use when simple objects no longer explain what we see. Instead of imagining the world as a collection of separate items, we can think of it as a collection of descriptions. A description is simply the way something appears when seen from a particular point of view. A rock has a shape, a movement has a trajectory, a heartbeat has a rhythm, and a thought has a structure of its own. Everything we know comes to us this way: not as raw matter, but as patterns that we interpret.

What is surprising is that the same thing can look completely different depending on the “dimension” of the description we use. A description with few dimensions may show us only the most obvious aspects, while a description with more dimensions may reveal relationships and hidden structures we never suspected. Imagine placing a lamp behind a glass sphere. If you look straight into the sphere, the lamp may appear twice. The world has not changed; your mode of description has. The sphere adds a kind of extra dimension to your viewpoint, splitting one appearance into two perfectly coordinated images. These two images are what the theory calls matching descriptions. They are two expressions of a single underlying reality, made visible because we have shifted to a richer level of observation.

This idea generalizes far beyond optical tricks. Nature hides many of its symmetries  (repeating structures, invariances, regularities) until we change the scale or the dimensional setting from which we look. A chaotic system may look random when viewed in ordinary space but reveal a clean, repeating pattern when represented in a higher-dimensional phase space. Two biological structures that seem unrelated, i.e., the branching of a lung and the branching of a plant root, may turn out to follow the same deep geometric logic. Even the way our brains recognize shapes, predict movements, or recall memories involves detecting these hidden correspondences. Matching descriptions, wherever they appear, show that what seemed separate may be two faces of the same structural pattern.

Many processes in the world also repeat in loops: breathing, heartbeats, sleep cycles, ecological rhythms, even habits of thought. In this framework such loops are called strings, i.e., paths that return to where they began. Strings are simply recurring patterns, and when we study them from a higher-dimensional angle, we often find matching descriptions hidden along their cycles. These are the symmetries that give the loop its stability and coherence.

To organize all the ways descriptions can vary, the theory introduces an abstract concept called the Monster. This name might sound dramatic, but here it simply refers to the total space of all possible descriptions, including those our universe never uses. Think of it as the ultimate map of all potential structures. Our physical universe occupies only a small region of this map. There may be many other regions filled with patterns we never encounter, yet this wider framework helps us understand what kinds of structures are possible and how the structures we observe relate to this larger landscape. Scientists regularly use similar ideas in physics and mathematics — configuration spaces, state spaces, manifolds, but the Monster is the largest such space we can imagine.

This perspective becomes especially powerful when we apply it to the brain. The brain does not simply record the world; it actively transforms simple descriptions into richer ones. When your eyes detect a cat, the initial signal is extremely limited: just light on the retina. But your brain quickly elevates this into a higher-dimensional pattern that includes recognition, memory, prediction, emotional tone, and conceptual structure. In this sense, your brain constantly turns single descriptions into matching descriptions, revealing correspondences that were not present at the sensory level. The “mental cat” is not a weaker version of the real cat. It is a structurally richer representation because it lives in a space with more dimensions, dimensions created by the brain itself. Attention acts as a spotlight deciding which descriptions should be expanded in this way, and time provides the sequence along which these expansions unfold.

Seen from this angle, the world is not primarily a collection of objects but a network of patterns that transform as we shift descriptive levels. What looks disconnected can become unified when viewed from the right dimension. What looks random may hide a structure that only appears when our viewpoint widens. What seems unique may turn out to have a counterpart we had never noticed.

The deeper message is simple: understanding any system (a physical process, a living organism, a thought) requires finding the level at which its hidden symmetries and matching descriptions become visible. At that level things that once seemed mysterious or unrelated suddenly make sense. If they still look unrelated, we may simply be looking from the wrong dimension. The world is full of structures waiting to be revealed. Many of them are not hidden at all; they are merely positioned one dimension above where we are currently looking.

 

 

 

 

NUGAE - A MAP OF EPISTEMIC STRATEGIES AT THE OUTERMOST LIMITS OF LANGUAGE

Language functions as the primary medium of scientific and philosophical inquiry, but it is also finite.  Yet there are moments when the inherited grammar (mathematical, logical or natural) ceases to hold. Equations diverge into singularities, models collapse into undecidability and words themselves dissolve into paradoxes. These limit-situations are not merely technical obstacles but epistemological thresholds, revealing that language is a finite instrument that delimits knowledge.

To engage with these thresholds, a variety of epistemic strategies have been developed. The following systematization arranges strategies into conceptual families, offering a provisional cartography of how inquiry navigates the edge of language to cope with “singularities”, i.e., breakdown points where established forms of description collapse or diverge.

 

1. Foundational strategies: extending and reinventing formalism

1.1 Extension of formal systems.  When established frameworks reach breakdown points, new symbolic systems to expand the formal apparatus are created to absorb anomalies.  Historical examples include the invention of complex numbers to handle square roots of negatives, non-Euclidean geometries to transcend Euclid’s fifth postulate or Hilbert spaces in quantum mechanics.  The singularity is thus recast not as an endpoint, but as a generative site for mathematical innovation.

1.2 Meta-formal strategies.  Instead of inventing entirely new systems, existing logics may be generalized. For instance, paraconsistent logics allow contradiction without collapse, fuzzy logics accommodate gradations of truth and category theory reorganizes structures at a higher level of abstraction.  These strategies domesticate limit-cases, offering rigor where classical formalism fails.

 

2. Pragmatic strategies: working with what is at hand

2.1 Pragmatic bricolage.  Scientists often employ ad hoc mixtures of symbols, diagrams, natural language and computer code to move forward.  These hybrid forms lack systematic unity but enable progress by leveraging multiple representational resources. Bricolage emphasizes functionality, reflecting the practical dimension of inquiry at the edge.

2.2 Simulation and visualization.  When verbal or mathematical language falters, visual and computational models step in.  Simulations can “show” dynamic processes and systems that resist concise description, while visualizations transform complexity into perceptual patterns. These strategies rely less on propositions and more on experience through representation.

2.3 Embodied practice.  Language is supplemented by embodied action: experiments, prototypes and manipulations of matter. Tacit knowledge, gestures and practices express what words cannot fully capture. Embodied practice emphasizes that knowing is not only linguistic, but also corporeal and situated.

 

3. Communal strategies: beyond the individual voice

3.1 Interdisciplinary translation.  Borrowing vocabularies from other disciplines provides new expressive tools.  For instance, physics adopts topological language from mathematics; biology draws from information theory and computation.  Translation generates hybrid idioms that extend beyond the limits of a single disciplinary language.

3.2 Collective dialogue.  Some boundaries can only be softened through the interplay of perspectives.  Dialogues, debates and communities of practice co-create new idioms that no single mind could devise. Language here evolves socially, highlighting the collective dimension of epistemic creativity.

 

4. Hermeneutic strategies: making sense with meaning beyond calculation

4.1 Metaphoric displacement.  Where formalism collapses, metaphor provides provisional scaffolding.  Scientific metaphors such as “black hole,” “genetic code,” or “molecular lock and key” function as bridges, rendering the incomprehensible graspable through analogy.  Metaphor is not literal truth but a vehicle for navigating the gap between language and phenomena.

4.2 Philosophical reflection.  Philosophy interrogates the conditions of language itself, asking whether the breakdown is ontological (in the world) or epistemic (in our categories).  This strategy shifts the focus from objects to the structures of thought, examining the limits of representation and the meaning of “unsayability.”  It re-situates singularities as questions about the relationship between language, thought and being.

4.3  Silence.  Silence acknowledges the unsayable without forcing premature articulation.  Wittgenstein’s dictum “whereof one cannot speak, thereof one must be silent”captures this stance.  Silence is not a void but a disciplined pause, leaving open the possibility of future languages.

 

Overall, our taxonomy suggests that the edge of language is not a terminal boundary but a generative field. No single approach can overcome this limit in isolation; yet, taken together, these strategies constitute a plural epistemic repertoire. Such a repertoire may open new avenues for addressing radical limit-situations of thought, including Being, consciousness and qualia.

 

QUOTE AS: Tozzi A.  20205.  Nugae -a map of epistemic strategies at the outermost limits of language.  DOI: 10.13140/RG.2.2.17515.40481

 

 

 

 

 

NUGAE - TRUTH AND SENSE AS A UNIFIED CATEGORY: COLLAPSING FALSE AND MEANINGLESS INTO TRUTHLESS

In contemporary philosophy of language and logic, there is a long-standing separation between what is false and what is meaningless. Classical semantics, following Frege and early Wittgenstein, allows for three categories: statements that are TRUE, statements that are FALSE and statements that are SENSELESS because they fail to properly refer or to form a coherent proposition. This threefold scheme allows the distinction among different failures in discourse, yet it also multiplies categories and forces scientists and philosophers to wrestle with the distinction between something that is false and something that simply does not make sense. In practice, both end up excluded from the realm of truth, but the analytic gap remains.

We propose to collapse this threefold distinction by defining senselessness as nothing other than truthlessness. Any statement that cannot be true, whether because it is factually incorrect or because it is semantically malformed, belongs to the same class. Truth becomes the only positive category, applying strictly to propositions that are both sense-bearing and empirically valid, while everything else is classified as truthless. This redefinition reduces the semantic landscape to two poles: truth and truthlessness. A statement like “the lac operon is upregulated by lactose” is true; “the lac operon is upregulated by glucose” and “the lac operon is upregulated by triangles” are both truthless. One is false within biology, the other is nonsense, but they occupy the same category of non-truth.

The advantages of our twofold approach are several. First, it simplifies the logical scheme, reducing ambiguity and the temptation to treat nonsense as if it had a privileged status. Second, it aligns scientific practice with epistemic hygiene: whether a claim fails by contradiction with data or by conceptual incoherence, its status is the same, namely, truthless. Third, it removes loopholes often exploited in pseudoscience or mysticism, where senseless formulations are smuggled in as though they could point to hidden truths.

Experimental tests of this framework can be pursued in linguistic corpora and scientific discourse. One could classify statements from biology, physics or medicine according to whether they bear sense and whether they correspond to empirical evidence.  Once senselessness is redefined as truthlessness, error rates in categorization are predicted to decrease and logical modeling of discourse becomes more efficient. In biology, Boolean or network models of gene regulation could be streamlined by mapping false and undefined states into a single truthless state, simplifying simulations and reducing computational overhead.

Beyond logical economy, this unification could recalibrate how we evaluate statements in science, philosophy and even machine learning. In artificial intelligence, it would discourage models from producing “plausible nonsense”, since senseless output is automatically labeled truthless. In education, it would highlight that truth is the primary positive category, while all other claims, whether false or meaningless, belong to a single, undifferentiated class.  In research, it could inspire new semantic filters for scientific publishing, automatically discarding truthless claims whether they are false or incoherent.

Future avenues may include formalizing our system into new logical calculi, designing algorithms that operationalize truthless detection and exploring its implications for epistemology, where the boundary between sense and truth becomes a single threshold rather than two.

QUOTE AS: Tozzi A.  2025.  Nugae -truth and sense as a unified category: collapsing false and meaningless into truthless.  DOI: 10.13140/RG.2.2.18147.82726

 

 

 

 

NUGAE - NATURE’S UNIFORMITY: RECONCILING SCIENTIFIC REALISM AND CONSTRUCTIVISM

The assumption of uniformity of nature has served as a cornerstone in philosophy of science for explanatory and predictive practices. Classical empiricism has treated this uniformity as either a brute fact or an indispensable postulate without which induction and scientific reasoning would collapse.  The various forms of scientific realism have assumed that nature possesses intrinsic order, laws describe preexisting regularities and successful prediction confirms our access to these uniformities.  Against this backdrop, Nelson Goodman’s constructivist claim that “the uniformity of nature we marvel at belongs to a world of our own making” undermines realist accounts.  If uniformity is not given in nature but arises from our symbol systems and classificatory practices, then the laws of science cannot be straightforwardly interpreted as mirrors of reality.  This raises the question of how to reconcile the undeniable success of science with the intriguing thesis that uniformity of nature is not inherent but constructed. 

We propose that uniformity of nature should be understood as an emergent relational feature arising from the interaction between symbolic schemes and the recurrent patterns of experience.  It results from the fit between worldmaking practices and environmental constraints, a fit that science continually refines through experimental feedback. Therefore, scientific laws function as instruments rather than mirrors: they stabilize our engagement with phenomena by organizing patterns of recurrence in ways shaped both by environmental structures and by human symbolic activity.  Regularities are neither simply discovered nor invented, but co-produced.  They become visible only when cognitive and symbolic frameworks are applied to the flux of phenomena, generating intelligible structures to test, revise and extend.  

To provide an example, think about weather forecasts: scientists use models refined to fit reality (like maps of air pressure or wind) to match repeating patterns in the atmosphere.  

Our proposal of uniformity of nature as a relational co-production between symbolic schemes and environmental constraints draws inspiration also from Dewey’s pragmatism, Putnam’s pluralism, van Fraassen’s constructive empiricism and contemporary cognitive science, particularly Andy Clark’s predictive processing and Richard Menary’s cognitive integration.  However, unlike these accounts, our aim is not to elaborate further philosophical insight, but rather to pragmatically suggest ways to generate testable predictions and outline directions for future research.

Our framework can be experimentally tested by analysing the performance of competing scientific models under conditions of novelty and stress. If uniformity were intrinsic, models should converge on the same structures regardless of symbolic framing. If it were arbitrary, success should be evenly distributed across frameworks.  In turn, our relational thesis predicts instead that models closer to the constraints of phenomena will outperform others in predictive and technological success, but only relative to the symbolic categories available at the time.

Testable hypotheses include that shifts in symbolic frameworks (for instance, from Newtonian to relativistic physics) alter what counts as uniformity without invalidating the pragmatic fit of earlier models in their proper domains. Further examples can be found in the transition from classical genetics to molecular biology, where, e.g.,  the symbolic shift from “hereditary factors” to “genes as sequences” redefined what counted as uniformity in inheritance, yet left Mendelian ratios

Predictive success will not rest on a single uniformity, but on the relational adequacy of the chosen symbolic scheme to the particular experimental condition. For instance, quantum field theory and string theory impose different symbolic categories and their relative success should be judged by the fit between the representational tools employed and the constraints revealed by high-energy experiments.

In epistemology, our theoretical perspective may provide a middle-grounded way to reframe debates about realism and constructivism, showing how scientific laws can be treated neither as mere inventions nor as mirrors of nature, but as relational achievements arising through interaction.

In cognitive science, it supports accounts of perception and reasoning as constructive processes tuned to environmental stability, echoing predictive processing theories (from Kant to Friston) in which brains impose generative models on sensory input, with success depending on how well those models capture recurrent constraints.

In artificial intelligence, our view suggests that machine learning systems may not uncover inherent laws, but create mappings between input structures and environmental constraints.  For example, in reinforcement learning, algorithms may succeed not by revealing hidden uniformities but by refining symbolic schemes to exploit stable patterns within data environments.

The same applies to natural language processing, where statistical models may not extract fixed linguistic laws but build relational fits between symbolic categories and communicative practices.  

In medicine, predictive models of disease spread or treatment response may succeed insofar as they align symbolic constructs like “risk factors” or “biomarkers” with actual environmental and biological constraints.

Future research may further formalize this view using tools from information theory to measure mutual information between symbolic frameworks and phenomena, or from network science to evaluate the structural alignment between representational models and empirical systems.

QUOTE AS: Tozzi A.  2025. Nugae -nature's uniformity: reconciling scientific realism and constructivism.  DOI: 10.13140/RG.2.2.21544.23041

 

 

 

 

 

NUGAE - BEING AND LIFE: A MATHEMATICAL FRAMEWORK FOR BIOLOGICAL EXISTENCE

The question of being has accompanied philosophy since its inception, from Parmenides’ assertion that “being is” and “non-being is not,” through Aristotle’s ontology of substance, to Heidegger’s attempt to retrieve the forgotten difference between being and entities. Traditionally, philosophy has treated being as the most universal and indeterminate concept, irreducible to any particular. Within metaphysics, God, the Idea of the Good or the Absolute have often been interpreted as the supreme expression of being. Yet this trajectory has remained largely detached from the empirical sciences, where the focus lies not on being in general but on specific entities and processes like molecules, cells organisms and ecosystems, all of which are concrete manifestations of life.  A rigorous definition of “biological being” has not been formalized in mathematical terms.

We suggest translating the philosophical notion of being into a mathematical/biological framework.  The key step is to treat being not as a metaphysical abstraction, but as existence within a domain. In mathematical logic, existence is expressed by the quantifier ∃, which asserts that “there exists” an object satisfying a predicate. In set theory, being can be interpreted as membership in a well-defined domain. Extending this to biology, we define an entity as biologically real if and only if it belongs to the domain of life and satisfies the minimal conditions of its organizational level. The definition may be expressed as follows:

BiologicalBeing(x)⟺(x∈D)∧Φ(x)

where D is the domain of biological entities and Φ(x) is the predicate that specifies the necessary conditions for existence at a given level. For molecules, Φ(x)  may correspond to a valid sequence with biochemical function; for cells, to occurrence of membranes, metabolism and replicative ability; for organisms, to the maintenance of homeostasis and membership in a population; for populations, to reproductive and ecological interaction; and for ecosystems, to flows of energy and cycles of matter. This provides a unified formalism:

∃x∈D:Φ(x)

which encapsulates biological being across scales of organization, from molecules to ecosystems.

Our framework has several advantages compared with other approaches. Unlike purely philosophical ontologies, it is anchored in mathematical precision and testable biological predicates. Unlike reductionist definitions of life privileging one level (e.g., the cell theory or the genetic central dogma), it scales across organizational hierarchies. Unlike purely empirical checklists of life’s properties, it provides a formal language that can be extended, compared and integrated with computational models.

To experimentally test our framework, one must operationalize the predicates Φ(x). For molecules, this means demonstrating that a candidate sequence not only exists chemically, but also performs a biological role, e.g., catalytic activity or regulatory function. For cells, experimental tests may involve assessing whether synthetic minimal cells meet the required predicates of membrane integrity, energy metabolism and reproduction. For organisms, testing involves verifying systemic properties like homeostasis or adaptability. For populations, ecological and genetic methods can assess reproductive interaction. Testable hypotheses include: artificially constructed entities meeting Φ(x) should be regarded as biologically real; modifications to entities removing one element of Φ(x) disprove their biological being; new levels of organization can be formally accommodated by redefining predicates without altering the overall formalism.

The potential applications are manifold. In synthetic biology, our approach could provide a rigorous criterion for determining when a synthetic construct is genuinely living. In astrobiology, it provides a mathematical definition to guide the search for extraterrestrial life by specifying predicates Φ(x) adapted to unknown environments. In systems biology, it enables the formal modeling of biological entities across scales in a consistent language. In philosophy of biology, it provides a way to reconcile metaphysical discourse on being with empirical science. Future research could extend our methodology  to evolutionary transitions, such as the origin of multicellularity, by treating each transition as a redefinition Φ(x) at a new level of organization. It could also be applied in computational biology to build formal ontologies that are mathematically grounded rather than descriptive.

In sum, by redefining being as existence within a biological domain formalized through quantifiers and predicates, we create a bridge between philosophy and empirical science. This mathematical ontology might providr a testable language for biological existence, unifying molecules, cells organisms, populations and ecosystems under the same existential principles.

 

QUOTE AS:  Tozzi A.  2025.  Nugae -being and life: a mathematical framework for biological existence. DOI: 10.13140/RG.2.2.14486.00328

 

 

 

 

 

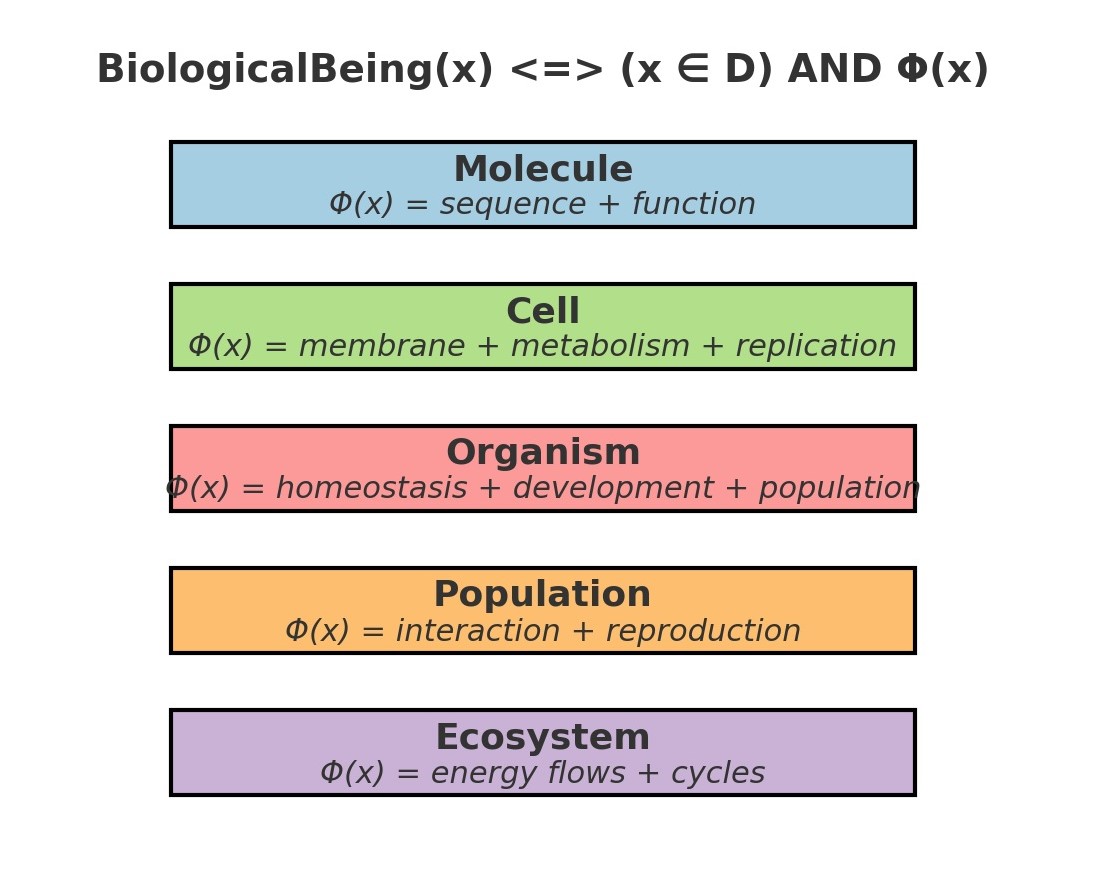
MATHEMATICAL TOPOLOGIES OF THOUGHT: A STRUCTURAL METHOD FOR ANALYZING PHILOSOPHICAL FRAMEWORKS

The intersection of mathematics and philosophy has traditionally focused on logic, set theory, and formal semantics. While these tools have proven effective for clarifying arguments and propositions, they often fail to capture the deeper relational and hierarchical structures underlying philosophical systems. Traditional methods like predicate logic, modal analysis, or set-theoretic classification are limited in assessing global structural coherence and dynamic interdependencies in complex conceptual frameworks.  To address these limitations, we propose a novel methodological approach that applies topological, algebraic, and probabilistic tools—specifically homotopy theory, sheaf cohomology, and convergence theorems—to the analysis of philosophical arguments. Rather than merely translating arguments into logical syntax, our method maps epistemic claims into mathematical spaces characterized by topological invariants and algebraic structures. This allows us to model conceptual coherence, continuity, and transformation across different systems of thought.

Our method treats philosophical doctrines as embedded structures in higher-dimensional conceptual spaces. Using tools like the Seifert–van Kampen theorem, Kolmogorov’s zero-one law, and the Nash embedding theorem, we may analyze how philosophical positions can be decomposed into substructures, reassembled through formal operations, and compared based on structural similarity or divergence. Homotopy equivalence provides a way to understand how epistemological models can be transformed while preserving essential properties. Meanwhile, probability theory enables a measure of epistemic stability or variability within those models.

This structural formalization provides several potential advantages. It allows for more rigorous comparison between philosophical frameworks, enables the visualization of conceptual dependencies, and provides metrics for evaluating internal consistency and coherence. The methodology opens the door to applications in artificial intelligence, where philosophical concepts could be operationalized within machine learning systems or automated reasoning engines. It also holds promise for digital humanities and the computational analysis of historical texts.  Our approach is distinct from existing techniques in its ability to preserve both local and global properties of philosophical structures, offering a new level of precision and formal clarity. Unlike purely logical or interpretive analyses, it introduces measurable, testable models of philosophical thought, setting the stage for future empirical investigations. Testable hypotheses include whether philosophical systems exhibiting homotopy equivalence correspond to similar cognitive models or whether certain topological features predict conceptual evolution.

Overall, this method represents a conceptual innovation to bridge mathematical formalism and philosophical analysis, providing a framework for future interdisciplinary research in epistemology, metaphysics, AI, and beyond.

 

QUOTE AS: Tozzi A. 2025. Topological and Algebraic Patterns in Philosophical Analysis: Case Studies from Ockham’s Quodlibetal Quaestiones and Avenarius’ Kritik der Reinen Erfahrung. Preprints. https://doi.org/10.20944/preprints202502.1518.v1.