Biology
Arturo Tozzi
Former Center for Nonlinear Science, Department of Physics, University of North Texas, Denton, Texas, USA
Former Computationally Intelligent Systems and Signals, University of Manitoba, Winnipeg, Canada
ASL Napoli 1 Centro, Distretto 27, Naples, Italy
For years, I have published across diverse academic journals and disciplines, including mathematics, physics, biology, neuroscience, medicine, philosophy, literature. Now, having no further need to expand my scientific output or advance my academic standing, I have chosen to shift my approach. Instead of writing full-length articles for peer review, I now focus on recording and sharing original ideas, i.e., conceptual insights and hypotheses that I hope might inspire experimental work by researchers more capable than myself. I refer to these short pieces as nugae, a Latin word meaning “trifles”, “nuts” or “playful thoughts”. I invite you to use these ideas as you wish, in any way you find helpful. I ask only that you kindly cite my writings, which are accompanied by a DOI for proper referencing.

NUGAE – HOW MODULAR BIOLOGICAL SURFACES SELF-ORGANIZE UNDER CONSTRAINTS: THE CASE OF ACHILLEA MILLEFOLIUM
Biological surfaces, from leaves to inflorescences, often appear ordered yet never perfectly crystalline. The balance between regularity and disorder is usually described qualitatively or reduced to broad concepts such as phyllotaxis or developmental modularity. In the case of composite flowers such as Achillea millefolium, the prevailing description is that many florets group into capitula which in turn form corymbs, thereby mimicking a single large flower. While this descriptive framework captures the visual impression, it fails to explain how individual florets interact with one another at the surface level, how their geometrical constraints shape collective arrangement and how these local rules translate into energetic economy and robustness.
Our proposal is to study Achillea capitula as modular surfaces able to self-organize under topological and energetic constraints. Each floret can be regarded as a discrete unit occupying a Voronoi-like territory. Its neighbors are defined through Delaunay triangulation, yielding a contact graph that encodes mechanical and spatial competition. Several parameters can quantify this system. First, the degree distribution of the contact graph tells us how many neighbors each floret maintains; its Shannon entropy measures variability in coordination, distinguishing homogeneous from heterogeneous packing. Second, the hexatic order parameter ∣ψ6∣|\psi_6|∣ψ6∣ quantifies local six-fold symmetry; values close to one indicate quasi-hexagonal packing in the capitulum interior, while lower values reveal defects or edge irregularities. Third, Voronoi cell areas and their coefficient of variation capture how equitably surface is partitioned among florets, while Voronoi entropy measures inequality in resource allocation. Fourth, nearest-neighbor distances and their distribution reflect mechanical pressure and polydispersity of florets.
Taken together, these parameters could define an “interaction signature” of each capitulum, which we expect to vary with position in the corymb, with light exposure and with environmental stress. A healthy capitulum should exhibit moderate to high ∣ψ6∣, low degree and Voronoi entropy and narrow nearest-neighbor distributions, whereas stressed or shaded ones should show breakdown of order and higher variability.
Compared with existing approaches focusing on large-scale phyllotaxis or visual mimicry, our framework provides quantitative, multi-scale and testable metrics of how modular floral units interact. It bridges geometry, topology and energetics without requiring genetic or biochemical data, thus offering a new layer of analysis complementary to developmental and ecological studies. This could allow the construction of empirical scaling laws between energy availability, growth constraints and surface organization.
Experimental validation can be pursued through high-resolution imaging of capitula across environmental conditions, automated segmentation of florets and computation of the metrics described. Manipulative experiments, such as selective removal of florets, shading of half-inflorescences or controlled nutrient limitation, should produce predictable shifts: decrease of ∣ψ6∣, increase in Voronoi entropy, broadening of nearest-neighbor distributions.
By understanding how modular surfaces self-organize, we could gain insight into fundamental principles of biological design. For plants, these arrangements may maximize visible surface and pollinator attraction while minimizing construction cost, distributing risk and maintaining robustness against damage. Beyond botany, our approach may apply to other modular systems: epithelial tissues where cells compete for surface, coral polyps forming colonies, bacterial biofilms spreading under spatial constraint. Potential applications range from crop science, where inflorescence packing efficiency correlates with yield and resilience, to biomimetic engineering, where controlled disorder can inspire low-energy materials or photonic structures. Future research may extend these metrics to dynamic imaging, capturing how packing entropy and hexatic order evolve over developmental time.
QUOTE AS: Tozzi A. 2025. nugae -how modular biological surfaces self-organize under constraints: the case of Achillea millefolium. DOI: 10.13140/RG.2.2.21198.52800


NUGAE – TOWARDS BACTERIAL SYNCYTIA: A FRAMEWORK FOR COLLECTIVE METABOLISM?
Experimental approaches to multicellular behavior and bacterial collectives usually emphasize surface interactions, nutrient gradients and community coordination via quorum sensing/extracellular molecules. We suggest that bacterial assemblies could be better understood as functional syncytia, where bacteria are integrated into shared metabolic/signaling units. The outer cells could act as the colony’s interface with the environment, absorbing stress, harvesting nutrients and sensing external cues, while the shielded inner cells could rely on buffered collective coupling. Inner cells, deprived of direct ligand access with the external milieu, could display underused and downregulated membrane receptors. Their physiology could be shaped by collective coupling: for instance, diffusible metabolites, continuously conveyed through nanotubes, vesicles or extracellular redox mediators, could replace receptor-driven signalling. Still, inner cells could shift between growth, quiescence or persistence in synchrony with the colony, maintaining viability and genetic continuity.
An interconnected network is achieved whose collective physiology cannot be reduced to single-cell behavior. A series of dynamical processes involving dynamic coupling point towards gradients and signals that are distributed across the population. For instance, electrical oscillations (e.g., potassium fluxes in Bacillus subtilis biofilms) propagate across millimeter scales, synchronizing growth and nutrient uptake between distant regions. These ion waves act as excitable media in which local perturbations propagate as traveling fronts, synchronizing collective activity in a manner analogous to action potentials coordinating responses across tissues. Metabolic cross-feeding (e.g., alanine cross-feeding in E. coli colonies) provides another form of dynamic coupling: inner cells, often hypoxic, secrete metabolites like alanine or lactate diffusing outward, while outer aerobic cells consume them, generating feedback loops of oscillating nutrient gradients. Vesicle trafficking and nanotube exchange (especially in Gram-negative bacteria) may introduce stochastic but impactful bursts of communication, where packets of proteins, plasmids or metabolites abruptly alter the state of neighboring cells. These coupled states may also generate bistability, with colonies toggling between high-growth and low-growth regimes depending on stress levels.
Altogether, the dynamics of a hypothetical bacterial syncytium could be expected to include oscillations, traveling waves, feedback-stabilized heterogeneity, stochastic bursts of exchange and regime shifts akin to phase transitions.
Compared with existing approaches that model biofilms as networks of communicating individuals, our perspective highlights shielding as a structural principle, explaining why inner populations maintain resilience under stress and how robust oscillations and gradients emerge as system-level properties.
Experimental validation could be pursued through microfluidic devices that enforce layered architectures, enabling direct observation of periphery-to-core propagation of signals. Fluorescent metabolite sensors could test whether inner cells respond to perturbations indirectly, while genetic knockouts disrupting nanotube or vesicle formation would probe the role of coupling in maintaining inner viability. It would also be feasible to investigate whether inner cells organize into complex networks characterized by distinctive topologies such as small-world architectures or scale-free distributions. By grounding the analysis in graph-mediated coupling and Laplacian dynamics, our approach may allow theoretical predictions to complement descriptive accounts of bacterial cooperation.
Predicted outcomes include measurable delays between outer and inner responses, reduced variance in inner activity under stress and traveling front patterns consistent with theoretical diffusion. A clear expectation is that colonies with intact coupling should buffer inner cells against environmental shocks, whereas decoupled populations would fragment into vulnerable individuals.
Our approach suggests that antibacterial strategies should not only target metabolic activity, but also disrupt the coupling mechanisms that improve collective resilience. Synthetic biologists might exploit bacterial syncytia to build engineered living materials with distributed sensing and metabolic stability. Over evolutionary timescales, our framework could provide a blueprint for viewing life as a continuum spanning solitary cells to fully integrated multicellular organisms. Microfluidic scaffolds could be employed to replicate outer-inner architectures and accelerate in vivo adaptive dynamics, positioning bacterial syncytia as an experimentally accessible midpoint for assessing both diversification and evolution.
QUOTE AS: Tozzi A. 2025. Nugae -towards bacterial syncytia: a framework for collective metabolism? DOI: 10.13140/RG.2.2.15224.92164


NUGAE - TOPOLOGICAL APPROACHES TO THE EVOLUTION OF SPECIES AND INDIVIDUALS
Many mathematical and conceptual approaches in evolutionary biology have incorporated geometric, relational and topological ideas: think to D’Arcy Thompson’s morphogenetic transformations, René Thom’s catastrophe theory, Rosen’s relational biology, Friston’s Free Energy Principle, Juarrero’s constraint closure, Barad’s agential realism, the Extended Evolutionary Synthesis, Walker and Davies’ informational perspective, Wolfram’s rule-based complexity, etc. Nevertheless, none of these frameworks provide a complete, explicitly topological general account of natural evolution.
We suggest to recast individuals and species as topological phenomena within a high-dimensional configuration manifold whose coordinates integrate genomic, phenotypic, ecological and developmental variables. An individual becomes a continuous trajectory maintaining local structural coherence, while a species is a connected component sustained by the turnover of constituent points. Selection is reformulated as the persistence of topological features under perturbation, extinction as the collapse of these features, reproduction as a cobordism linking trajectories in higher-dimensional spaces, while adaptation as the occupation of regions where compatibility conditions, formalizable in sheaf theory, are satisfied.
The advantage of this formulation lies in replacing fitness and goal-based narratives with persistence of invariants such as Betti numbers and lifetimes of cycles, yielding a unified, scale-independent mathematical description compatible with nonequilibrium thermodynamics and information theory. Still, it is empirically tractable via persistent homology robust to noise and incomplete data.
Methods to test this topological framework include embedding longitudinal multi-omics, phenotypic and environmental datasets into state spaces, computing Vietoris–Rips or witness complexes, tracking persistent features through time, running controlled microbial evolution experiments with environmental perturbations and simulating rule-based or agent-based models to check whether invariant structures emerge under non-teleological rules.
Testable hypotheses include that speciation corresponds to the birth of new connected components and shifts in Betti-0, that developmental canalization corresponds to stabilization of higher-dimensional cycles across ontogeny, that evolutionary convergence reflects attraction to the same homology class, that persistence lifetimes of invariants outperform classical fitness metrics in predicting lineage survival.
Potential applications include forecasting evolutionary trajectories from invariant structure, identifying ecological niches as persistent regions in morphospace, detecting early-warning signals of collapse through topological transitions, designing synthetic organisms for structural persistence and building evolutionary algorithms to optimize invariant persistence without teleological accounts. Future research could develop category-theoretic underpinnings linking constraint closure to sheaf cohomology, relate Markov blanket boundaries to nerve complexes of interaction graphs, derive thermodynamic limits on invariant lifetimes and implement scalable topological data analysis pipelines for eco-evolutionary dynamics.
QUOTE AS: Tozzi A. 2025. Topological Approaches to the Evolution of Species and Individuals. DOI: 10.13140/RG.2.2.35506.52163

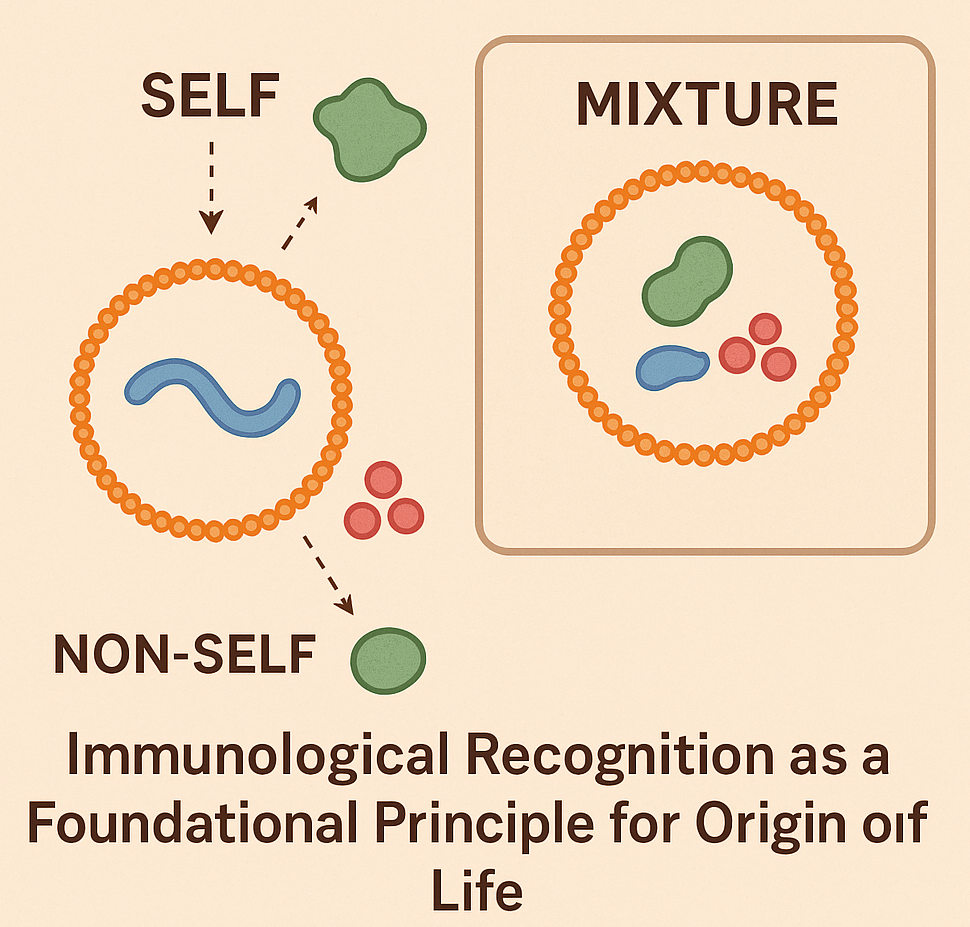
NUGAE - WAS IMMUNITY THERE FIRST? A NEW PERSPECTIVE ON LIFE’S ORIGIN
Most prevailing models of the origin of life focus on the formation of self-replicating molecular systems as the key step toward the occurrence of the first cells, emphasizing the role of either metabolism, compartmentalization or replication of RNA and other polymers. Yet most origin-of-life models overlook a fundamental property of all living systems, i.e., the ability to distinguish self from non-self, a core immunological function central to biology. We propose to integrate the immunological principle of identity maintenance to explore whether primitive forms of molecular recognition were a necessary prerequisite for the emergence of life. We hypothesize that even the earliest protocells or molecular systems required a minimal capacity to recognize and preserve their own components while excluding or neutralizing harmful elements, as this function would have been essential for achieving stability, accurate replication and long-term persistence.
To experimentally explore the theoretical immunological functions of protocells and reconstruct minimal conditions for self/non-self discrimination, we propose using lipid vesicles as model systems of protocells encapsulating well-defined “self” molecules such as RNA analogs, short peptides or labeled polymers. These protocells would be introduced into environments containing a complex mixture of “non-self” molecules, e.g., synthetic analogs of potentially parasitic or disruptive agents. By varying the chemical nature, charge and sequence specificity of both self and non-self molecules, we could assess how protocells respond in terms of stability, retention of contents and selective uptake or exclusion. Molecular crowding agents and environmental stressors (e.g., pH shifts, ionic fluctuations) would simulate potential early Earth environments. This setup would allow us to test whether physical, chemical or molecular properties (e.g., selective permeability, primitive recognition motifs, molecular competition, binding specificity or environmental noise) may enable protocells to preserve their molecular identity over time. Fluorescence tagging and microscopy would track the interaction dynamics, while leakage assays and molecular degradation measurements would quantify vesicle integrity and self-preservation. Additional experiments could incorporate engineered membrane proteins or synthetic receptors to test primitive recognition motifs and mimic early forms of selective binding.
Overall, we introduce the perspective that life may have required an early form of molecular “recognition” preceding, or occurring alongside, replication. This perspective may provide insight into how primitive identity mechanisms evolved into complex immune functions and could also guide future studies on molecular discrimination, rise of parasitism and early strategies for coping with environmental stress.
QUOTE AS: Tozzi A. 2025. Nugae -Was Immunity There First? A New Perspective On Life's Origin. DOI: 10.13140/RG.2.2.13691.22561

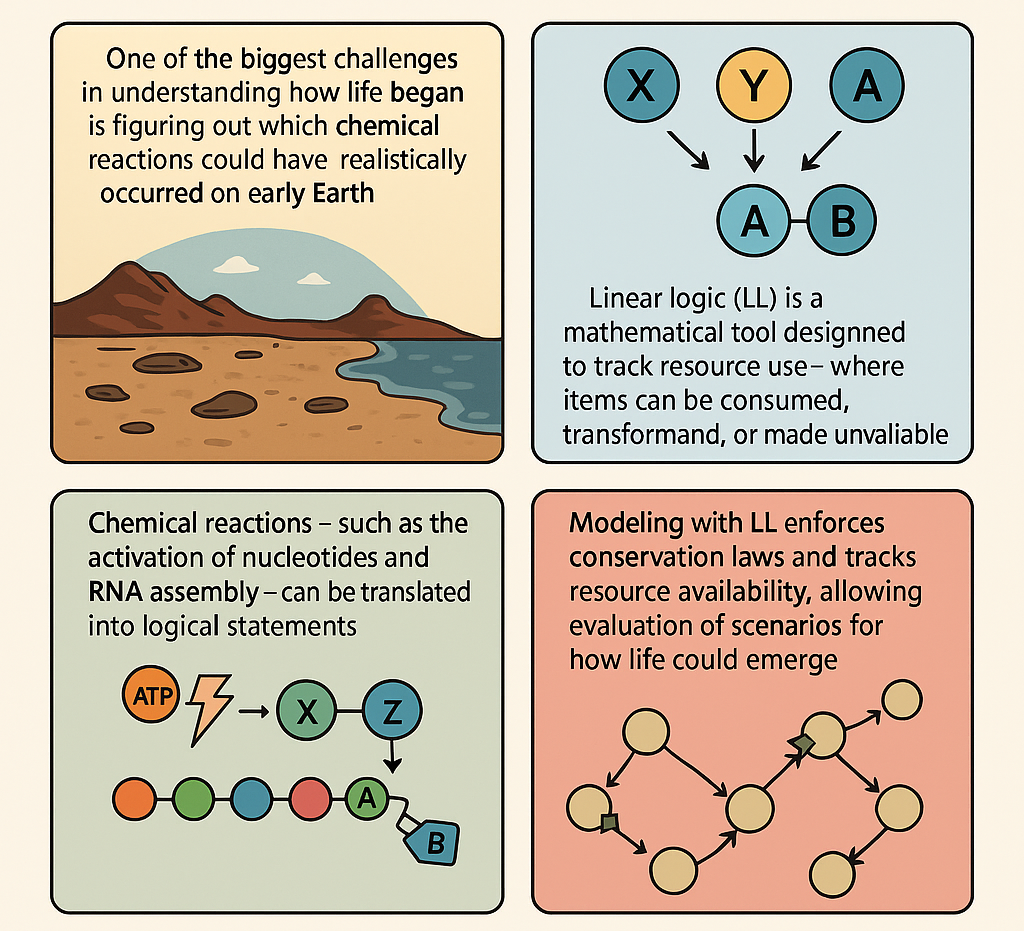
LACKING RESOURCES AT THE ONSET OF LIFE: USING LINEAR LOGIC TO MODEL HOW LIFE BEGAN
One of the biggest challenges in understanding how life began is figuring out which chemical reactions could have realistically occurred on early Earth. Most models assume that molecules like RNA could self-replicate, but they often don’t take into account how limited resources—like energy or building blocks—might have constrained these processes. To address this, we can use a tool from mathematical logic called Linear Logic (LL), which is designed to track how resources are used and transformed. Linear Logic is different from ordinary logic. In classical logic, you can reuse assumptions as many times as you like. But real-world chemistry doesn’t work that way. If you use up a molecule in a reaction, it’s gone—you can’t just use it again. LL reflects this principle. It treats every item as something that can be consumed, changed, or made unavailable, which is exactly what happens in chemical reactions. For example, in LL, you can’t use the same unit of energy to fuel multiple reactions at once—just like in real chemistry.
The method works by translating chemical reactions—such as the activation of nucleotides, RNA assembly, and even the transition from RNA to DNA—into logical statements within a LL system. These statements represent how many molecules are available, what is needed for a reaction, and what gets produced. By doing this, one can build a complete logical map of a possible pathway toward life, while keeping track of everything being used along the way. This LL-based framework doesn't just mimic chemistry, rather it enforces strict rules that mirror conservation laws, making sure nothing comes from nothing. You can simulate different environmental conditions (like temperature changes or radiation) and see how they affect molecular stability or replication. You can also test what happens when resources are scarce or when catalysts are added.
In short, this approach offers a formal and testable way to evaluate how life could have emerged from non-living matter. It doesn’t aim to simulate every detail but instead provides a resource-sensitive framework for checking whether a proposed sequence of reactions is even possible. Scientists can use this logic-based method to rule out impossible scenarios, highlight promising ones and ultimately guide experiments that explore the origins of life in a more structured and realistic way.
QUOTE AS: Tozzi A. 2025. Prebiotic Resource Constraints and the Origin of Life: A Linear Logic Framework. bioRxiv 2025.03.23.644802; doi: https://doi.org/10.1101/2025.03.23.644802

WHY ORDER MATTERS IN BIOLOGY: A MATHEMATICAL WAY TO UNDERSTAND SEQUENCE-DEPENDENT SYSTEMS
Many biological and evolutionary processes depend not just on what happens, but on the exact order in which things happen. For instance, the order in which transcription factors bind to DNA can decide whether a gene is turned ON or stays OFF. Similarly, in evolution, the sequence in which mutations occur can change the outcome—even if the same mutations are present. This “order sensitivity” makes biological systems non-commutative, meaning reversing steps can lead to different results. Traditional biological models often ignore or simplify this directionality. To address this, the paper applies a mathematical tool called the Wedderburn–Artin theorem. This theorem helps break down complex non-commutative structures into simpler, manageable pieces called matrix blocks. The authors treat biological events (like binding or mutations) as algebraic operations and construct a custom algebra to represent them. Then, using Wedderburn’s decomposition, they divide this algebra into smaller parts that each represent a unique “behavioral module.”
The method was applied to two scenarios:
- Gene regulation: The model simulates how the order of transcription factor binding (like A before B or B before A) affects gene expression. It showed that only one order (A → B) strongly activates the gene, while others have little or no effect.
- Evolutionary mutations: The study modeled different mutation orders (e.g., A → B → C vs. C → B → A) and their effects on trait expression. Again, only one specific order led to full trait development, highlighting how mutation history matters.
In both cases, the algebraic method successfully sorted different sequences into functional categories. It also reduced the complexity of analyzing all possible sequences by grouping them into smaller, interpretable modules.
This mathematical framework doesn’t simulate timing or continuous changes, but it’s powerful for understanding systems where the order of steps is critical. The approach could be used in fields like genetics, systems biology, and synthetic biology to uncover which event orders are essential and which are redundant. In short, this paper shows how tools from abstract algebra can help explain and simplify the logic behind real biological systems—especially when the order of events changes everything.
QUOTE AS: Tozzi, Arturo. Applications of Wedderburn's Theorem in Modelling Non-Commutative Biological and Evolutionary Systems. Preprint. Posted April 3, 2025. https://doi.org/10.1101/2025.04.03.647006.

